Помогите, пожалуйста, исследовать ряд на сходимость:
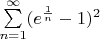
Моя попытка решения такова:
1. Установил, что

.
Следовательно, достаточное условие расходимости не выполняется.
2. Установил, что ряд является знакоположительным:

3. Попробовал применить признак Д'Аламбера:

т.к.

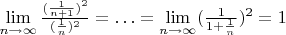
Т.е. признак Д'Аламбера использовать нельзя.
4. Можно доказать, что

, но интегральный признак Коши применить не удается. WolframAlpha говорит, что интеграл общего члена ряда не выражается через элементарные функции.
5. Остается использовать признаки сравнения рядов. С каким рядом сравнивать?
Также сообщу, что WolframAlpha сообщает, что ряд сходится.