Необходимо найти область сходимости функционального ряда

.
По признаку Даламбера получаем:

.
Следовательно, данный ряд сходится (при этом абсолютно) для всех

удовлетворяющих неравенству

, т.е. для

.
При

и
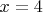
ряд принимает вид

. Это гармонический ряд. Он расходится.
Нужно ли доказывать, что данный ряд расходиться для

?