Атлас римановой поверхности

[MChagall]

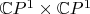
Для данной римановой поверхности в $\mathbb{C}P^1\times \mathbb{C}P^1$ задать голоморфный атлас:
1) $w^3=z^2+1$
2) $w=\sqrt{1-\sqrt[3]{z^2}}$.

Правильно ли я понимаю, что мне надо покрыть всю плоскость областями (картами), на которых задать координаты, через которые голоморфно выразить $w,z$?
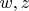
Если да, то
1) Предлагаю шесть карт.
Первые четыре следующего типа
1. Верхняя полуплоскость с разрезом по лучу $[i, +\infty)$;
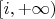
2. Нижняя полуплоскость с разрезом по лучу $(-\infty, -i]$;
3. Полуплоскость $\operatorname{Re} z< 1$ с разрезом по лучу $\operatorname{Im} z=i, \operatorname{Re} z \leqslant 0$;
4. Полуплоскость $\operatorname{Re} z> -1$ с разрезом по лучу $\operatorname{Im} z=-i, \operatorname{Re} z \geqslant 0$;
В этих картах координатой берём $z$, а $w=\sqrt[3]{z^2+1}$; склейка карт тождественным отображением.

Карта №5. Вводим координату $\zeta$: $z=i+\zeta^3; w=\zeta \sqrt[3]{2i+\zeta^3}$;
Карта №6. Вводим координату $\xi$: $z=-i+\xi^3; w=\xi \sqrt[3]{-2i+\xi^3}$.

Всё ли верно? Что забыл/не понял?

[DeBill]

MChagall в сообщении #1310579 писал(а):

Что забыл

Везде - следовало сказать, какую из ветвей корня надо брать.
Для 5 и 6 - не указана область определения параметризации

[MChagall]

Везде берём главную ветвь корня ($\sqrt[3]{1}=1$).
5. $\left\lvert \zeta\right\rvert<\sqrt[3]{2}$
6. $\left\lvert \xi\right\rvert<\sqrt[3]{2}$.
Так верно?

[DeBill]

Ага. Только насчет 5,6 не уверен - с глобальной инъективностью $w$. Можно было, перестрахуясь, взять малый диск.

[MChagall]

А с точкой $z=\infty$ не надо ничего делать?

[DeBill]

MChagall в сообщении #1310914 писал(а):

А с точкой $z=\infty$ не надо ничего делать?

Ох, я был сильно невнимателен: конечно, надо. И там ведь у нас ветвление...
И: в 3 и 4 - что-то нехорошее, там вторая точка ветвления мешается.
И: что-то маловато областей у Вас в 1 и 2...И если, как Вы написали, выбирать везде главную ветвь - ведь не склеится что-то там...

MChagall в сообщении #1310579 писал(а):

В этих картах координатой берём $z$, а $w=\sqrt[3]{z^2+1}$

Которую из трех ветвей? Может, Вы имели в виду - все три? Тогда число областей следует утроить...
Может, вместо 1-4 взять три области (односвязных), с разрезами, соединяющими точки ветвления (их у нас - три) (и - в трех экз. каждую...)

[MChagall]

DeBill в сообщении #1311030 писал(а):

Может, вместо 1-4 взять три области (односвязных)

Если я правильно понял, то Вы предлагаете такие области:
1. $\mathbb{C}\setminus[-i,+\infty)$
2. $\mathbb{C}\setminus(-\infty,i)$
3. $\mathbb{C}\setminus((-\infty,-i)\cup(i, +\infty))$.
Такие?

[DeBill]

Да. Может, и получится...

[MChagall]

Пришло время разобраться со 2).
$P(z, w)=z^2-(1-w^2)^3=0$
Проблемными точками являются
a) точки, в которых $P(z,w)=P_w(z,w)=P_z(z,w)=0$
Это $z=0, w=\pm 1$
b) точки ветвления $z=\pm 1;w=0$

a) Тут предлагается ввести $z=\xi^3; w=\sqrt{1-\xi^2}$, $\xi\in (-1;1)$
Верно это?
b) А здесь $z=\sqrt{(1-\zeta^2)^3}$. Тогда $w=\zeta$. То есть координатой можно взять $w$, но так как мне дан не $P(z,w)$, то надо идти через замену $z$.
Верно здесь?