Свойства оценки

[artey]

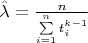
Здравствуйте. Нужна помощь в решении задачи:нужно исследовать свойства оценки $\hat \lambda = \frac{n}{{\sum\limits_{i = 1}^n {\mathop t\nolimits_i^{k - 1} } }}$ (несмещенность, состоятельность), полученной методом максимального правдоподобия для параметра $\lambda$ для распределения Вейбулла с плотностью $f(t) = \lambda {t^{k - 1}}k{e^{ - \lambda {t^{k - 1}}}}(t \geqslant 0,\lambda > 0,k > 0)$.
Определения из лекций:${\hat \theta _n}={\hat \theta _n}({x_1},...,{x_n})$ является состоятельной оценкой для параметра $\theta$, если она сходится по вероятности ${\hat \theta _n}\xrightarrow[{n \to \infty}]{P}\theta$ к истинному значению параметра с ростом объема выборки.
${\hat \theta _n}={\hat \theta _n}({x_1},...,{x_n})$ является несмещенной оценкой для параметра $\theta$, если ее математическое ожидание совпадает с истинным значением параметра т.е. $E{\hat \theta _n}= \theta$.
В Википедии написано, что математическое ожидание для распределения Вейбулла равно $\lambda \Gamma (1 + \frac{1}{k}) $, где $\Gamma$ - это гамма-функция.
Натолкните пожалуйста на мысль как решать данное задание?Хотя бы как проверить несмещенность?

[Otta]

artey в сообщении #1310359 писал(а):

с плотностью $f(t) = \lambda {t^{k - 1}}k{e^{ - \lambda {t^{k - 1}}}}(t \geqslant 0,\lambda > 0,k > 0)$

Оно плотностью не является.

[artey]

Otta в сообщении #1310360 писал(а):

artey в сообщении #1310359 писал(а):

с плотностью $f(t) = \lambda {t^{k - 1}}k{e^{ - \lambda {t^{k - 1}}}}(t \geqslant 0,\lambda > 0,k > 0)$

Оно плотностью не является.

Это у распределения такая плотность по заданию. А мне нужно исследовать свойства оценки $\hat \lambda = \frac{n}{{\sum\limits_{i = 1}^n {\mathop t\nolimits_i^{k - 1} } }}$ (несмещенность, состоятельность), полученной методом максимального правдоподобия.

[Otta]

artey
Еще раз: это вообще не плотность. Перепишите правильно.

[artey]

Otta в сообщении #1310393 писал(а):

artey
Еще раз: это вообще не плотность. Перепишите правильно.

Вот изначальное задание из задачника:

[Otta]

Не, ну я что сделаю. Проверьте сами. Интеграл от плотности по прямой каким должен быть? И сделайте вывод.
Исправить, чтобы была плотность для указанных значений параметров, нетрудно, но и оценка тогда будет другая.

[artey]

Нужно для полученной оценки сделать, другой не надо.

[Otta]

Вы же оценку по плотности получали. Напишите нормальную плотность (если проверяли, то наверняка поняли, где надо исправить) и посчитайте для нее оценку, это второе, кстати, входит в задание.

А сейчас Вы хотите пахать на танке: трактора не дали. Ваше право.

[artey]

Здравствуйте, по поводу несмещенности, сделал так:$\lambda = \frac{1}{\mu }\ $, $\mu = \frac{{\sum\limits_{i = 1}^n {t_i^{k - 1}} }}{n}$, $E\widehat \mu = E(\frac{{\sum\limits_{i = 1}^n {t_i^{k - 1}} }}{n}) = \frac{1}{n}\sum\limits_{i = 1}^n {Et_i^{k - 1} = } \frac{1}{n}\sum\limits_{i = 1}^n {\lambda \Gamma (1 + \frac{1}{k}) = } \lambda \Gamma (1 + \frac{1}{k}) = ...?$ Как дальше равенство продолжить?

[Otta]

Несмещенность оценки $\mu$ никак не поможет в несмещенности оценки $\lambda$. Надо сразу заниматься нужной оценкой.
И надо начинать с верно выписанной плотности.

[artey]

Otta в сообщении #1313689 писал(а):

Несмещенность оценки $\mu$ никак не поможет в несмещенности оценки $\lambda$. Надо сразу заниматься нужной оценкой.
И надо начинать с верно выписанной плотности.

Мне преподаватель сказал так сделать. Чему будет это равно $\lambda \Gamma (1 + \frac{1}{k})$ подскажите, пожалуйста.

[Otta]

О господи. Извините, я не могу выполнять требования некомпетентного человека, Ваши ли они лично или чьи-то еще. Мне еще не все равно.

artey в сообщении #1313695 писал(а):

$\lambda \Gamma (1 + \frac{1}{k})$

Вот этому и равно, улучшений не будет. Никакого отношения к решению это выражение не имеет, но по сравнению с остальными его минусами это мелочи.

Вам надо научиться решать задачу или научиться выполнять требования преподавателя?
Если второе, в этих условиях я пас.

-- 20.05.2018, 19:37 --

Если доберетесь до задачи, а не до требований:
1. Поправьте плотность. Не умеете сами - попросите преподавателя. Это не плотность.
2. Найдите оценку лямбда для новой плотности.
3. Занимайтесь матожиданием именно этой оценки, а не чем-то еще, - все остальное бессмысленно.