ЦК и УК матрицы.

[Alexey Rodionov]

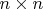
$A $ - матрица $n \times n $. Если ее первая и последняя строки ортогональны (как векторы из $C^n$) первому и последнему столбцам, уберем их всех из $A $ и продолжим процесс. Матрица называется центрально - квадратной (ЦК) если ее можно преобразовать в "пустую". Пример отличной от нуля ЦК: $a_{n,1} \not = 0 $, все остальные компоненты равны нулю.
Очевидно, можно "стягивать" к элементам $a_{1,1}, a_{1,n}, a_{n,1}, a_{n,n}$, определяя угольно-квадратные (УК) матрицы.
Задачи: исследовать свойства ЦК, УК и матриц из пересечения. Все образы навеянные абревиатурами считать случайными совпадениями и безжалостно отметать.
Варианты: добавить к требованиям определений отличие от нуля и равенство норм убираемых строк и столбцов. Если требовать равенства норм отдельно для строк и отдельно для столбцов, следует говорить о прямоугольных, а не о квадратных матрицах. Если же нормы отличны от нуля, но между собой не равны - это странные прямоугольные матрицы.

[Alexey Rodionov]

Уточняю: каждая упомянутая строка ортогональна всякому пресловутому столбцу. Чтобы квадратик получился.

[arseniiv]

Каким свойством должна обладать угольно-квадратная, я лично не понял.

-- Пт май 04, 2018 23:27:31 --

Вместо крайних берутся центральные пара строк и столбцов?

[Alexey Rodionov]

Я собирался брать те же самые, но выбрасывать строку и столбец не прилегающие к углу. Вот не знаю, стоит ли. Вроде, все слишком просто получается.

[arseniiv]

(Раз уж я тут уже написал, добавлю, что не вижу от этих понятий много пользы. Просто как упражнение в себе — ну, может быть. А приложений у таких вещей как-то не представляется, больно уж искусственно. Может, потому в теме пока так безлюдно.)

[Alexey Rodionov]

Какие там приложения. Просто забавно показалось.