_DEADMANИтак, Вас сейчас интересует интеграл

.
Вот эти множители в числителе и знаменателе:

и

- наверное как-то связаны между собой. Наверное не зря они оба обращаются в нуль при
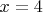
. Наверное можно один из них выразить через другой, если формулу нужную вспомнить - и что-то упростится. И, кстати говоря, какой лучше через какой?
А после этого можно будет использовать вот что:
Учтите при этом, что, если

, то можно написать

при

и от какого-то множителя избавиться.
Только не нужно вот так фантазировать:
или здесь уже можно сравнивать с

?
Если Вы что-то с чем-то хотите "сравнивать", то должны знать, на какие теоремы и признаки собираетесь при этом опираться.