В общем, я так понимаю, у вас всё же некоторые значения, индексированные
двумя числами:

А то вы не очень-то понятно сначала описали. В будущем это описывать можно очень просто: последовательность

элементов множества

есть просто некоторая функция
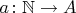
, так что «

-мерная последовательность» элементов из

есть функция
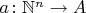
. Для конечных вместо соответствующих копий

берутся его начальные отрезки.
Возвращаясь к исходной теме, какой угодно многомерный массив можно развернуть в линейный, так что все комбинаторные числа, никак не зависящие от нахождения элементов, скажем, в одинаковых строках или столбцах, будут такими же как для развёрнутого.