Найти интеграл с помощью бета и гамма функции

[nortonouls]

Итак, приветствую всех, прошу помощи. Вот такое задание дали на первом курсе по матану:
Решить с помощью В-функции и Г-функции (для этого подкорректировать пределы интегрирования):

$$\int\limits_0^5\frac{dx}{(25+x^2)\cdot \sqrt{25+x^2}}$$

Мои шаги (на пределы пока что забил):
$\int\frac{dx}{(25+x^2)^{3/2}}=\int \frac{dx}{(25)^{3/2} \left(1+\frac{x^2}{25}\right)^{3/2}}=(*)$
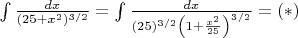
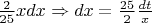
Сделаем замену: $\frac{x^2}{25}=t \Rightarrow x=5\sqrt{t}$. Тогда $\frac{2}{25}xdx \Rightarrow dx=\frac{25}{2} \frac{dt}{x}$. Получаем

$$(*)=\frac{1}{50}\int \frac{dt}{(1+t)^{3/2} \cdot \sqrt{t}}$$

Ну и собственно вот, я в тупике. Ведь по идее для В-функции перед $t$ должен быть минус. Пробовал заменять $\frac{x^2}{25}=-t$, но тогда, во-первых, под корнем будет число с минусом, когда выражаем отсюда $x$, а во-вторых, тогда минус появляется уже там, где он не нужен.
Пожалуйста, подскажите, что делать

[thething]

Интересно, зачем здесь бета-функция, особенно на первом курсе, если Эйлерова подстановка $\sqrt{x^2+25}=t-x$ решает проблему?

[nortonouls]

thething в сообщении #1305134 писал(а):

Интересно, зачем здесь бета-функция, особенно на первом курсе, если Эйлерова подстановка $\sqrt{x^2+25}=t-x$ решает проблему?

Потому что вот такой преподаватель. Задание было решить тремя способами: двумя любыми и один обязательно бета-функцией. Двумя я уже решил, а этим - пока не могу

[Vince Diesel]

Докажите, что при определенных предположениях относительно $a$ и $b$

$$ \int_0^{\infty } \frac{dt}{t^a (1+t)^b} =B(1-a,a+b-1). $$

[provincialka]

Интеграл ведь будет от $0$ до $+\infty$, а не до $5$?
Такие пределы имеют интересную особенность: если $t$ меняется от $0$ до $+\infty$, то $1/t$ от $+\infty$ до $0$, а $\frac1{1+t}$ -- от $1$ до $0$.

[thething]

nortonouls
Можно использовать второе определение бета функции $B(x,y)=\int\limits_{0}^{+\infty}\frac{s^{x-1}}{(1+s)^{x+y}}ds$. Из исходного определения бета функции $B(x,y)=\int\limits_{0}^{1}t^{x-1}(1-t)^{y-1}dt$ данное получится, если выполнить замену $t=\frac{s}{1+s}$

Вам надо так подкорректировать пределы, чтобы в итоге вот тут

nortonouls в сообщении #1305089 писал(а):

Получаем

$$(*)=\frac{1}{50}\int \frac{dt}{(1+t)^{3/2} \cdot \sqrt{t}}$$

получились нужные пределы от 0 до $\infty$

[nortonouls]

Всем спасибо, получилось!