Задача:
Показачть, что любой кососимметрический определитель
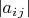
четвертого порядка с

является квадратом целого числа.
Попытки решения:
Я доказал, что для нечетного порядка определители кососимметрических матриц равны нулю, исходя из равенства определителей обычной матрицы и транспонированной. Думал над алгебраическими дополнениями, в нашей матрице порядка 4, обнаружил, что

для

. Но никак не могу прийти к квадрату.