Статья, страница 13 писал(а):
Цитата:
Answer only if you are
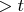
confident, since mistakes are penalized
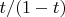
points, while correct answers receive

point, and an answer of “I don’t know” receives 0 points.
There are several natural values of

including
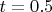
(penalty

),
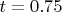
(penalty

), and
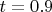
(penalty

).
Ну ладно, авторы статьи могут поделить

на

и получить

, хотя попросить кого-то вычитать статью перед выкладыванием не помешало бы. Но если уж вы пересказываете статьи, еще и перефразируя, то можно же заметить, что получается бред?
(
Rasool, это камень частично в Ваш огород, и сильно - в адрес канала)
Тогда выгоднее всегда говорить "Я не знаю", независимо от степени уверенности
Нет, если вероятность правильного ответа больше

, то выгоднее давать предполагаемый ответ.
На этапе предобучения задача модели – всегда предложить вероятное продолжение текста. У нее нет варианта сказать "я не знаю".
Модель учится предсказывать вероятность следующего токена. И если следующий токен - дата рождения, то тут оптимальное распределение - близкое к равномерному (точнее, к частоте реальных дат рождения, которая не совсем равномерная).
У модели есть опция продолжить текст "День рождения Ивана Ивановича" токенами "я не знаю". Но, поскольку в обучающей выборке подобные продолжения встречаются редко, то этому продолжению будет приписана не очень большая вероятность.
И да, модели для некоторых практических задач дообучают говорить "я не знаю". Меняя обучающую выборку так, чтобы в ней было много таких примеров.
А кстати, как эту степень уверенности модели считают
В статье деталей нет, есть ссылки, но тут надо долго разбираться. Из общих соображений, я бы предположил, что тут речь либо просто о вот таком промпте для модели, либо об обучении с подкреплением, в котором награда за ответ вот такая.
Тут еще рядом есть интересный вопрос о внешних и внутренних вероятностях. Модель - это просто распределение на текстах, позволяющий эффективно считать условное распределение при условии префикса. Но модели еще можно задать вопрос
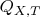
"а какая будет вероятность токена

при условии префикса

?". Она, скорее всего, напечатает какое-то число

. Но вероятности
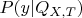
и вероятности
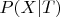
не обязаны быть как-то связаны. Что означает, что "внутренняя" уверенность модели может сильно отличаться от "внешней".
(и в этом нет ничего удивительного, можно еще у человека спрашивать, какие нейроны в коре его мозга активируются)