Теорема Вейерштрасса (функция многих переменных)

[VitDer]

Добрый вечер!

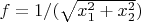
В ряде публикаций встретил "необычную" (как мне показалось) формулировку теоремы К. Вейерштрасса. А именно: "Непрерывную функцию нескольких переменных $f(x_1,x_2,...,x_n)$, заданную на ограниченном множестве Q, можно равномерно приблизить последовательностью полиномов $P(x_1,x_2,...,x_n)$ со сколь угодной заданной точностью $e$." Что же это означает? Пусть $f=1/(\sqrt{x_1^2+x_2^2})$. Тогда я могу заниматься подбором коэффициентов $A_1,A_2,A_3,...$ многочлена $P=A_1\cdot x_1 +A_2\cdot x_2+A_3\cdot x_1\cdot x_2+...$ , будучи уверен, что смогу их "подрегулировать" до нужной точности $e$?

Если это так, то хорошо. Однако в русскоязычных (да и зарубежных) учебниках и пособиях по мат. анализу и теории приближений функций никак не могу найти формулировку т. Вейерштрасса для функции 2-х и более переменных. Может быть, кто-нибудь знает "авторитетный источник", на который можно будет сослаться?

P.S. Предполагаю, что ответ содержит теорема Стоуна-Вейерштрасса, но с теорией, которая в ней используется, практически не знаком.

Спасибо заранее.

[demolishka]

Только лишь ограниченностью не обойтись, нужна компактность. Количество переменных роли не играет, называется это утверждение теоремой Стоуна-Вейерштрасса.

-- 12.04.2018, 05:18 --

VitDer в сообщении #1303399 писал(а):

Тогда я могу заниматься подбором коэффициентов $A_1,A_2,A_3,...$ многочлена $P=A_1\cdot x_1 +A_2\cdot x_2+A_3\cdot x_1\cdot x_2+...$ , будучи уверен, что смогу их "подрегулировать" до нужной точности $e$?

Теоретически --- да (для любой наперед заданной точности гарантируется, что некоторый многочлен приближает данную функцию с этой точностью).

[VitDer]

Я так и предполагал. Плохо то, что многочлен раскладывается в бесконечный ряд, и оценить степень многочлена, необходимую для обеспечения данной точности приближения не представляется возможным ... Поэтому придётся настраивать бесконечное число коэффициентов $A_1,A_2,...$, а это уже никуда не годится ... Может быть, имеет смысл обратиться к полиномам Бернштейна, но есть ли они для многомерного случая ...

[ewert]

demolishka в сообщении #1303420 писал(а):

Только лишь ограниченностью не обойтись, нужна компактность.

Компактность, естественно, не нужна: коль скоро можно приблизить на замыкании -- тем более можно и на исходном множестве.

VitDer в сообщении #1303458 писал(а):

Плохо то, что многочлен раскладывается в бесконечный ряд,

Ничего плохого -- многочлен просто не нужно раскладывать в ряд. И, кстати, теорема Вейерштрасса ровно ничего не говорит о разложении в ряд по многочленам -- она утверждает лишь возможность приближения.

VitDer в сообщении #1303458 писал(а):

Поэтому придётся настраивать бесконечное число коэффициентов $A_1,A_2,...$

Не придётся, т.к. с бесконечными наборами никто никогда не работает, если решаются вычислительные задачи.

VitDer в сообщении #1303458 писал(а):

Может быть, имеет смысл обратиться к полиномам Бернштейна,

Нет смысла -- многочлены Бернштейна страшно далеки от эффективности. Их достоинство в другом -- в исключительной конструктивности построения. Однако приближённые методы дают качественные результаты гораздо быстрее.

[DeBill]

ewert в сообщении #1303463 писал(а):

Компактность, естественно, не нужна: коль скоро можно приблизить на замыкании -- тем более можно и на исходном множестве.

Компактность, конечно, нужна : ибо кто сказал, что на замыкании приближаемая функция непрерывна (да и вааще определена)?