Изучая геометрическую интерпретацию случайных величин дошел до следующего факта.
Пусть

- вектор случайная величины,

- прямая констант. Спроектировав веткор случайной величины

на плоскость в которой лежат

и

мы получим следующее равенство:

.

Решив систему мы уравнений мы получили, что

Дальше мы находим расстояние между нашим вектором случайной величины и проекцией его на плоскость.

Последнее равенство для меня не очевидно, мне кажется должно быть

, но исходя из дальнейших рассуждений автора учебника, складывается впечатление что здесь нет опечатки. Почему же свернулость в
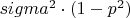
??