Неформальная ZFC — теория, в которой существует единственный тип объектов — множества и единственный предикат

. Множества и отношение принадлежности подчинены следующим девяти аксиомам ZF1–ZF9.
ZF1 (Аксиома экстенсиональности). Два множества равны,

, если они содержат одни и те же элементы, т.е. если

.
Определим отношения включения

как

. В этих обозначениях

в том и только том случае, когда

и

.
Множество, не содержащее ни одного элемента, называется пустым множеством и обозначается

.
ZF2 (Аксиома существования). Существует пустое множество.
ZF3 (Аксиома неупорядоченных пар). Для любых двух вещей

и

существует множество

, единственными элементами которого являются

и

.
ZF4 (Аксиома объединения). Для любого множества множеств

существует объединение

.
ZF5 (Аксиома бесконечности). Существует такое множество

, что
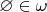
и для любого
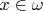
имеем
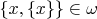
.
ZF6 (Аксиома подстановки). Допустим, что для любого

существует единственный

такой, что
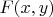
. Тогда для любого множества

существует единственное множество

, состоящее из всех

таких, что
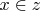
и
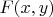
.
ZF7 (Аксиома степени). Для любого множества

существует множество

такое, что

в том и только том случае, когда

.
ZF8 (Аксиома выбора). Пусть
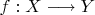
— сюръективное отображение. Тогда существует отображение

такое, что для любого

имеет место равенство

.
ZF9 (Аксиома регулярности). Пусть

. Тогда существует такой элемент

, что для любого элемента

выполняется
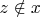
.
В отличие от формальной ZFC, здесь нет какого-то фиксированного алфавита и не определены правила построения формул. Вместо этого, предложения формулируются на естественном языке, а единственным критерием правильности формул служит их понятность. Также, теория не содержит логических аксиом и не специфицирует правил вывода — а значит, она не является теорией первого порядка.