Добрый день!
Пытаясь разобраться с понятием степени, в т.ч. с рациональным показателем, пришел к следующему.
В учебнике дается следующее определение степени с рациональным показателем:

(не знаю, есть ли на форуме возможность записи корня с показателем, поэтому в правой части пишу в виде дроби

). Обоснование: Одно из основных свойств степени для степени с рациональным показателем, а именно равенство

выполняется только при указанном условии (определении).
Но ведь с другой стороны, равенство

, выполняется только при
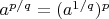
.
Кроме того, n-я степень числа с натуральным показателем - это произведение n-го количества сомножителей, равных этому числу. И по аналогии с этим определением, степень числа с натуральным показателем

можно было бы определить как произведение

-го количества сомножителей, равных степени этого числа с показателем

, т.е. как раз как
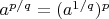
.
Мой вопрос состоит в следующем: Если степень с рациональным показателем означает совершение над ее основанием последовательно операций возведения в степень с показателем, равным числителю рац.показателя, и извлечения корня с показателем, равным знаменателю рац.показателя, то в каком порядке они должны выполняться?
Конечно, ввиду установленного правила о том, что степень с рац.показателем определена только при неотрицательном основании, а также введением понятия арифметического корня, т.е. установлением взаимно-однозначного соответствия между показателем степени и ее значением, данный вопрос утрачивает значение.
Предполагаю, что наиболее точным определением степени с рациональным показателем в самом общем виде, является ее определение, как значение показательной функции?!
Подскажите, что бы почитать на эту тему?