Такой абстрактный вопрос.
Возьмем множество решений, например,

рассматриваемое как некоторое подмножество в (например, опять же)
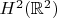
.
Так вопрос, что это будет за подмножество. Например, связно ли?
Можно ли задать на нем (компонентах связности) CW-комплекс? посчитать какие-то гомологии?
Можно ли задать что-то подобное многообразию?
В общем, что-то, касающееся свойств как объекта в целом.
Мне так, навскидку, представляется, что должно быть связно (берем гомотопию соответствующих условий задачи Коши, скажем).
А как задать клеточное разбиение, и можно ли - никаких идей.
Теплопроводность просто как пример, интересно, есть ли какие-то такие результаты, касающиеся чего-то бесконечномерного.