Обосновать изоморфизм

[npetric]

Обосновать изоморфизм:
$\frac{\mathbb{Z}[x]/(x^2-5)}{(2)} \simeq \frac{\mathbb{Z}[x]}{(2,x^2-5)}$

Пользуемся третьей теоремой об изоморфизме:
$\frac{\mathbb{Z}[x]/(x^2-5)}{(2,x^2-5)/(x^2-5)} = \frac{\mathbb{Z}[x]/(x^2-5)}{(2)} \simeq \frac{\mathbb{Z}[x]}{(2,x^2-5)}$

Меня интересует первое равенство, которое, строго говоря, изоморфизм, и неясно, как его обосновать. Ясно, что в этом конкретном случае можно предъявить явным образом гомоморфизм с нужным ядром, но это не интересно.

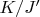
Иначе говоря, что понимать под $K/J'$, если:
$J \subset K, J' \subset K', J \simeq J', K \simeq K'$,...
и еще что-то, до чего я пока дойти не могу, и что изображает связь идеалов с их кольцами: $\mathbb{Z}/(2) \not \simeq \mathbb{Z}/(3)$

Какой формализм за этим стоит?