для случая, когда обе аналитические кривые -- дуги окружностей разных радиусов
Ну, это не критично: инверсией (др.линейным отображением) окружности можно перевести в прямые, и тогда из свойства "симметрия" для др.-линейных следует, что все хорошо.
Но в общем случае?
Без ограничения общности, можно считать (в некой карте

) кривую
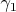
совпадающей с осью абсцисс (и тогда симметрия относительно нее есть просто комплексное сопряжение

), а в некоторой карте

-кривую
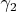
совпадающей с осью абсцисс (и тогда симметрия относительно нее есть также комплексное сопряжение

), надо лишь сказать, что

. Условие совпадения симметричных кривых тогда можно записать так: отображение

переводит вещ. ось в себя. Это равносильно тому, что

, откуда

,или

, где

. Но это - сто пудов - не всегда так.
Rem. Ясно, что "аналитический тип" пары вещ-аналитических кривых, пересекающихся под нужным углом, полностью задается отображением

(имеющим нужную линейную часть). Так что случай совпадения - описывается ровно теми

, для которых

- "триволюция"
Пример:

, где

(не проверял - громоздко, но, думаю, не получится триволюция. Забавно, что для вещественно-аналитического

, да и для дробно -линейного (в этих случаях как раз легко считаются композиции), - получится)