(Оффтоп)
Я когда-то давно задавал вопрос о том, как считается погрешность коэффициентов линейной регрессии. Однозначных ответов я тогда не получил, видимо, потому что задавал плохой вопрос, и нужно было поучиться, чтобы задать вопрос хороший.
Итак, есть выборка измеренных величин

. Хотим получить оценку по методу наименьших квадратов:

, где ошибка

(величины
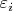
— реализации случайной величины

), как

. Лемма о коэффициентах линейной регрессии утверждает:
1) величины

;
2) величины

независимы;
3) величина

;
4) величины

,
где обозначения такие:

,

,
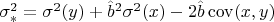
, угловые скобки - выборочное среднее,

— выборочная дисперсия величины

(может быть коллизия, но

без аргументов есть дисперсия нормально распределённой ошибки, как условлено вначале),

— выборочная ковариация,

(

) — распределение Стьюдента (Пирсона) с

степенями свободы.
Из утверждения 4) легко вытащить доверительные интервалы для

и

(для к-тов регрессии). Как оценить дисперсии

и

истинных значений коэффициентов, которые выражаются через

, которую мы не знаем? Из третьего утверждения, скажем, можно вытащить равенство типа такого:

где

---

-квантиль распределения Пирсона с

степенями свободы. Из этого равенства можно верхнюю оценку получить, а
уточнить как-то можно?