DeBillСпасибо вам, после вашей подсказки мои рассуждения были следующие
начинал с

перевернул дробь
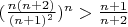
Затем

И вот тут, при применения неравенство Бернулли возникли вопросы
я решил преобразовать правую часть.
как известно, неравенство Бернулли

дальше
вместо

у меня

Правая часть

Где-то тут неточность, ошибка . Потому что
если сравнить

и

при

то

осталось разобраться с этим моментом
Вопрос, как изменить знак неравенства Бернулли, если применять конкретно к моему примеру?
дальше все получилось, искомое неравенство удалось доказать.