Есть пространственная кривая

. Если из каждой точки кривой опустить перпендикуляр на плоскость

, эти отрезки сформируют часть цилиндрической поверхности, «сверху» органиченной исходной кривой, а «снизу» — её проекцией на плоскость

.
Пример для
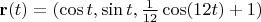
:

(Код Wolfram Language)
Код:
f[t_] := {Cos[t], Sin[t], 1/12 Cos[12 t] + 1}
Show[ParametricPlot3D[{f[t], ReplacePart[3 -> 0][f[t]]}, {t, 0, 2 \[Pi]}, PlotStyle -> Gray], Graphics3D[{Thick, Gray, Table[Line[{f[t], ReplacePart[3 -> 0][f[t]]}], {t, 0, 2 \[Pi], 2 \[Pi]/96}]}], Boxed -> False, Axes -> None]
В данном простом примере получаем часть прямого кругового цилиндра, снизу ограниченную окружностью, сверху — некоей кривулькой.
Вопрос: как задать такую поверхность параметрически, уравнениями и неравенствами? Понятно, что, напрмер, часть цилиндра, отсекаемая двумя параллельными плоскости

плоскостями, задаётся как
![$\mathbf{r}(u, v)=(\cos v, \sin v, u), v \in [0, 2\pi], u \in [u_1, u_2]$ $\mathbf{r}(u, v)=(\cos v, \sin v, u), v \in [0, 2\pi], u \in [u_1, u_2]$](https://dxdy-02.korotkov.co.uk/f/5/8/b/58b27ea536bf13ff9d3562471a97bfee82.png)
. Но дальше у меня пока затык.