10 на 10 не режется на 1 на 4.
Вот ключ к разгадке. 1 минимальная длина. В целочисленном

этой стороной можно замостить его и по вертикали, и по горизонтали. А так как

, то вторая, большая сторона должна делить оставшуюся сторону нацело.
Если в процессе деления возникнет прямоугольник с нецелой второй стороной, то тут уже ничего не поделаешь: меньше чем 1 натуральное число не бывает.
Т.е. дело просто в масштабе.
Допустим,

, а

. п.1 выполнен.
Но теперь всё разделим на 3.

,

- замостить нельзя!
А вот

уже можно.
Т.о. остаётся одно условие: одно из чисел

должно делиться на меньшее из
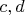
, а второе - на оставшееся.