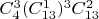Здравствуйте! Неуверен в правильности рассуждений
Из колоды в 52 выбираются 5 карт. Сколько есть таких пятерок, где: а) достоинств ровно 4; б) 2 карты
имеют одно достоинство, 2 –другое, а пятая — третье; в) достоинств ровно 3 и три карты имеют одно достоинство; г) три карты имеют одно достоинство, а две оставшиеся — другое;
а) Рассматриваю 4 масти, выбираю одну масть и беру из нее 2 карты разных достоинств

теперь на оставшиеся 3 места беру карты из других мастей такого же достоинства, как в первой масти

итог:
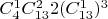
б) Рассмотрим какие-то две масти и выберем по одной карте из них одного достоинства

аналогично для других двух мастей

и последняя карта

итог:

в) Три карты имеют одно достоинства: берем 3 масти из них по одной карте одного достоинства
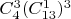
а другую часть условия не понял, это разве не одно и тоже?
г) Получается так же берем 3 масти и по одной карте из них одного достоинства
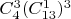
и две оставшиеся

итог: