|
Последний раз редактировалось B@R5uk 01.02.2018, 13:46, всего редактировалось 3 раз(а).
Переработал свой алгоритм в конечный автомат на четыре состояния. 0) В нулевом осуществляется сдвиг единички влево, то есть удаление предыдущего элемента и добавление текущего. В это состояние можно попасть, если на предыдущем шаге был перелёт. 1) В первом состоянии просто добавляется текущий элемент. После выполнения итерации в этих состояниях осуществляется проверка на перелёт и на достижение самого первого элемента. В последнем случае осуществляется переход ко 2) второму состоянию, которое является промежуточным перед третьим и в котором удаляются из суммы все повторы первого элемента. 3) В третьем состоянии осуществляется поочерёдное удаление уже добавленных в сумму элементов и проверка на недолёт. Поскольку эти проверки теперь делаются в основном цикле по одной на итерацию, то я вернул возможность поймать нужную сумму в процессе проверок, сразу выдать её и пропустить обработку целой пачки состояний. Код получился такой:
import java.util.*;
public class StudySubsetSearch16 {
private static final Random rng = new Random();
private static final int maxRand = 4;
private static final int size = 12;
private static final int[] values = new int[size];
private static final int[] cumulativeSums = new int[size];
private static final int[] entryFlags = new int[size];
private static final int[] entryToTheRight = new int[size];
private static final int[] entryToTheLeft = new int[size];
private static int firstRepeats, state, index, nextEntryIndex;
private static int sum, tagetSum;
public static void main(String[] args) {
int n, value, lastValue, previousEntryIndex, totalSum;
int repetitions, subsetsNumber, matchCount, iterationCount;
boolean isFlagged;
for (n = 0; size / 4 > n; ++n) {
values[n] = 2 + maxRand + rng.nextInt(4 * maxRand);
}
for (; size > n; ++n) {
values[n] = 2 + rng.nextInt(maxRand);
}
Arrays.sort(values);
index = -1;
entryToTheLeft[0] = index;
lastValue = values[0];
sum = lastValue;
cumulativeSums[0] = sum;
isFlagged = true;
repetitions = 0;
subsetsNumber = 1;
for (n = 1; size > n; ++n) {
value = values[n];
sum += value;
cumulativeSums[n] = sum;
if (lastValue != value) {
index = n - 1;
subsetsNumber *= repetitions + 2;
if (isFlagged) {
firstRepeats = repetitions;
isFlagged = false;
}
repetitions = 0;
} else {
++repetitions;
}
entryToTheLeft[n] = index;
lastValue = value;
}
if (isFlagged) {
firstRepeats = repetitions;
}
subsetsNumber *= repetitions + 2;
tagetSum = sum / 3 + rng.nextInt(maxRand);
System.out.println(Arrays.toString(values));
System.out.println(Arrays.toString(cumulativeSums));
System.out.println(Arrays.toString(entryToTheLeft));
System.out.println(firstRepeats);
System.out.println();
nextEntryIndex = size;
index = size - 1;
sum = 0;
state = 1;
matchCount = 0;
iterationCount = 0;
isFlagged = true;
while (isFlagged) {
switch (state) {
case 0:
previousEntryIndex = entryToTheLeft[nextEntryIndex];;
if (-1 == previousEntryIndex) {
state = 2;
break;
}
entryFlags[nextEntryIndex] = 0;
sum -= values[nextEntryIndex];
nextEntryIndex = entryToTheRight[nextEntryIndex];
index = previousEntryIndex;
case 1:
entryFlags[index] = 1;
sum += values[index];
entryToTheRight[index] = nextEntryIndex;
nextEntryIndex = index;
--index;
display(entryFlags, -1, sum, tagetSum);
if (tagetSum <= sum) {
if (tagetSum == sum) {
System.out.println(" Match!");
++matchCount;
} else {
System.out.println(" Overshot");
}
state = 0;
} else {
System.out.println();
state = 1;
}
if (-1 == index) {
state = 2;
}
break;
case 2:
do {
++index;
entryFlags[index] = 0;
sum -= values[index];
} while (firstRepeats > index);
nextEntryIndex = entryToTheRight[firstRepeats];
state = 3;
default:
if (size == nextEntryIndex) {
display(entryFlags, -1, sum, tagetSum);
System.out.println(" End");
isFlagged = false;
break;
}
entryFlags[nextEntryIndex] = 0;
sum -= values[nextEntryIndex];
index = entryToTheLeft[nextEntryIndex];
nextEntryIndex = entryToTheRight[nextEntryIndex];
totalSum = cumulativeSums[index] + sum;
display(entryFlags, index, totalSum, tagetSum);
if (tagetSum > totalSum) {
System.out.println(" Undershot");
} else if (tagetSum == totalSum) {
System.out.println(" Match!");
++matchCount;
} else {
System.out.println();
state = 1;
}
}
++iterationCount;
}
System.out.println();
System.out.print("Subsets found: ");
System.out.println(matchCount);
System.out.print("Itrations made: ");
System.out.println(iterationCount);
System.out.print("Subsets total number: ");
System.out.println(subsetsNumber);
}
private static void display(int[] array, int index, int sum, int tagetSum) {
int n, size;
size = array.length;
for (n = 0; index >= n; ++n) {
System.out.print("x");
}
for (; size > n; ++n) {
System.out.print(array[n]);
}
System.out.print(" -> ");
System.out.print(String.format("%2d", sum));
System.out.print(" (");
System.out.print(tagetSum);
System.out.print(")");
}
}
Результаты он выдаёт приблизительно такие:
[2, 2, 2, 2, 2, 4, 4, 4, 5, 7, 16, 20]
[2, 4, 6, 8, 10, 14, 18, 22, 27, 34, 50, 70]
[-1, -1, -1, -1, -1, 4, 4, 4, 7, 8, 9, 10]
4
000000000001 -> 20 (23)
000000000011 -> 36 (23) Overshot
000000000101 -> 27 (23) Overshot
000000001001 -> 25 (23) Overshot
000000010001 -> 24 (23) Overshot
000010000001 -> 22 (23)
000110000001 -> 24 (23) Overshot
xxxxxxxxxxx0 -> 50 (23)
000000000010 -> 16 (23)
000000000110 -> 23 (23) Match!
000000001010 -> 21 (23)
000000011010 -> 25 (23) Overshot
000010001010 -> 23 (23) Match!
xxxxxxxx0010 -> 38 (23)
000000010010 -> 20 (23)
000000110010 -> 24 (23) Overshot
000010010010 -> 22 (23)
000110010010 -> 24 (23) Overshot
xxxxx0000010 -> 26 (23)
000010000010 -> 18 (23)
000110000010 -> 20 (23)
001110000010 -> 22 (23)
011110000010 -> 24 (23) Overshot
xxxxxxxxxx00 -> 34 (23)
000000000100 -> 7 (23)
000000001100 -> 12 (23)
000000011100 -> 16 (23)
000000111100 -> 20 (23)
000001111100 -> 24 (23) Overshot
000010111100 -> 22 (23)
000110111100 -> 24 (23) Overshot
xxxxx0011100 -> 26 (23)
000010011100 -> 18 (23)
000110011100 -> 20 (23)
001110011100 -> 22 (23)
011110011100 -> 24 (23) Overshot
xxxxx0001100 -> 22 (23) Undershot
xxxxxxxx0100 -> 29 (23)
000000010100 -> 11 (23)
000000110100 -> 15 (23)
000001110100 -> 19 (23)
000011110100 -> 21 (23)
000111110100 -> 23 (23) Match!
xxxxx0110100 -> 25 (23)
000010110100 -> 17 (23)
000110110100 -> 19 (23)
001110110100 -> 21 (23)
011110110100 -> 23 (23) Match!
xxxxx0010100 -> 21 (23) Undershot
xxxxx0000100 -> 17 (23) Undershot
xxxxxxxxx000 -> 27 (23)
000000001000 -> 5 (23)
000000011000 -> 9 (23)
000000111000 -> 13 (23)
000001111000 -> 17 (23)
000011111000 -> 19 (23)
000111111000 -> 21 (23)
001111111000 -> 23 (23) Match!
xxxxx0111000 -> 23 (23) Match!
xxxxx0011000 -> 19 (23) Undershot
xxxxx0001000 -> 15 (23) Undershot
xxxxxxxx0000 -> 22 (23) Undershot
000000000000 -> 0 (23) End
Subsets found: 6
Itrations made: 72
Subsets total number: 384
[2, 2, 3, 3, 4, 4, 5, 5, 5, 8, 9, 17]
[2, 4, 7, 10, 14, 18, 23, 28, 33, 41, 50, 67]
[-1, -1, 1, 1, 3, 3, 5, 5, 5, 8, 9, 10]
1
000000000001 -> 17 (23)
000000000011 -> 26 (23) Overshot
000000000101 -> 25 (23) Overshot
000000001001 -> 22 (23)
000000011001 -> 27 (23) Overshot
000001001001 -> 26 (23) Overshot
000100001001 -> 25 (23) Overshot
010000001001 -> 24 (23) Overshot
xxxxxx000001 -> 35 (23)
000001000001 -> 21 (23)
000011000001 -> 25 (23) Overshot
000101000001 -> 24 (23) Overshot
010001000001 -> 23 (23) Match!
xxxx00000001 -> 27 (23)
000100000001 -> 20 (23)
001100000001 -> 23 (23) Match!
010100000001 -> 22 (23)
110100000001 -> 24 (23) Overshot
xx0000000001 -> 21 (23) Undershot
xxxxxxxxxxx0 -> 50 (23)
000000000010 -> 9 (23)
000000000110 -> 17 (23)
000000001110 -> 22 (23)
000000011110 -> 27 (23) Overshot
000001001110 -> 26 (23) Overshot
000100001110 -> 25 (23) Overshot
010000001110 -> 24 (23) Overshot
xxxxxx000110 -> 35 (23)
000001000110 -> 21 (23)
000011000110 -> 25 (23) Overshot
000101000110 -> 24 (23) Overshot
010001000110 -> 23 (23) Match!
xxxx00000110 -> 27 (23)
000100000110 -> 20 (23)
001100000110 -> 23 (23) Match!
010100000110 -> 22 (23)
110100000110 -> 24 (23) Overshot
xx0000000110 -> 21 (23) Undershot
xxxxxxxxx010 -> 42 (23)
000000001010 -> 14 (23)
000000011010 -> 19 (23)
000000111010 -> 24 (23) Overshot
000001011010 -> 23 (23) Match!
000100011010 -> 22 (23)
001100011010 -> 25 (23) Overshot
010100011010 -> 24 (23) Overshot
xx0000011010 -> 23 (23) Match!
xxxxxx001010 -> 32 (23)
000001001010 -> 18 (23)
000011001010 -> 22 (23)
000111001010 -> 25 (23) Overshot
010011001010 -> 24 (23) Overshot
xxxx01001010 -> 28 (23)
000101001010 -> 21 (23)
001101001010 -> 24 (23) Overshot
010101001010 -> 23 (23) Match!
xx0001001010 -> 22 (23) Undershot
xxxx00001010 -> 24 (23)
000100001010 -> 17 (23)
001100001010 -> 20 (23)
011100001010 -> 22 (23)
111100001010 -> 24 (23) Overshot
xx0100001010 -> 21 (23) Undershot
xx0000001010 -> 18 (23) Undershot
xxxxxx000010 -> 27 (23)
000001000010 -> 13 (23)
000011000010 -> 17 (23)
000111000010 -> 20 (23)
001111000010 -> 23 (23) Match!
010111000010 -> 22 (23)
110111000010 -> 24 (23) Overshot
xx0011000010 -> 21 (23) Undershot
xxxx01000010 -> 23 (23) Match!
xxxx00000010 -> 19 (23) Undershot
xxxxxxxxxx00 -> 41 (23)
000000000100 -> 8 (23)
000000001100 -> 13 (23)
000000011100 -> 18 (23)
000000111100 -> 23 (23) Match!
000001011100 -> 22 (23)
000011011100 -> 26 (23) Overshot
000101011100 -> 25 (23) Overshot
010001011100 -> 24 (23) Overshot
xxxx00011100 -> 28 (23)
000100011100 -> 21 (23)
001100011100 -> 24 (23) Overshot
010100011100 -> 23 (23) Match!
xx0000011100 -> 22 (23) Undershot
xxxxxx001100 -> 31 (23)
000001001100 -> 17 (23)
000011001100 -> 21 (23)
000111001100 -> 24 (23) Overshot
010011001100 -> 23 (23) Match!
xxxx01001100 -> 27 (23)
000101001100 -> 20 (23)
001101001100 -> 23 (23) Match!
010101001100 -> 22 (23)
110101001100 -> 24 (23) Overshot
xx0001001100 -> 21 (23) Undershot
xxxx00001100 -> 23 (23) Match!
xxxxxx000100 -> 26 (23)
000001000100 -> 12 (23)
000011000100 -> 16 (23)
000111000100 -> 19 (23)
001111000100 -> 22 (23)
011111000100 -> 24 (23) Overshot
xx0111000100 -> 23 (23) Match!
xx0011000100 -> 20 (23) Undershot
xxxx01000100 -> 22 (23) Undershot
xxxx00000100 -> 18 (23) Undershot
xxxxxxxxx000 -> 33 (23)
000000001000 -> 5 (23)
000000011000 -> 10 (23)
000000111000 -> 15 (23)
000001111000 -> 19 (23)
000011111000 -> 23 (23) Match!
000101111000 -> 22 (23)
001101111000 -> 25 (23) Overshot
010101111000 -> 24 (23) Overshot
xx0001111000 -> 23 (23) Match!
xxxx00111000 -> 25 (23)
000100111000 -> 18 (23)
001100111000 -> 21 (23)
011100111000 -> 23 (23) Match!
xx0100111000 -> 22 (23) Undershot
xx0000111000 -> 19 (23) Undershot
xxxxxx011000 -> 28 (23)
000001011000 -> 14 (23)
000011011000 -> 18 (23)
000111011000 -> 21 (23)
001111011000 -> 24 (23) Overshot
010111011000 -> 23 (23) Match!
xx0011011000 -> 22 (23) Undershot
xxxx01011000 -> 24 (23)
000101011000 -> 17 (23)
001101011000 -> 20 (23)
011101011000 -> 22 (23)
111101011000 -> 24 (23) Overshot
xx0101011000 -> 21 (23) Undershot
xx0001011000 -> 18 (23) Undershot
xxxx00011000 -> 20 (23) Undershot
xxxxxx001000 -> 23 (23) Match!
xxxxxx000000 -> 18 (23) Undershot
000000000000 -> 0 (23) End
Subsets found: 20
Itrations made: 158
Subsets total number: 864
[2, 3, 3, 3, 3, 4, 4, 4, 5, 10, 10, 21]
[2, 5, 8, 11, 14, 18, 22, 26, 31, 41, 51, 72]
[-1, 0, 0, 0, 0, 4, 4, 4, 7, 8, 8, 10]
0
000000000001 -> 21 (26)
000000000011 -> 31 (26) Overshot
000000001001 -> 26 (26) Match!
000000010001 -> 25 (26)
000000110001 -> 29 (26) Overshot
000010010001 -> 28 (26) Overshot
100000010001 -> 27 (26) Overshot
xxxxx0000001 -> 35 (26)
000010000001 -> 24 (26)
000110000001 -> 27 (26) Overshot
100010000001 -> 26 (26) Match!
x00000000001 -> 23 (26) Undershot
xxxxxxxxxxx0 -> 51 (26)
000000000010 -> 10 (26)
000000000110 -> 20 (26)
000000001110 -> 25 (26)
000000011110 -> 29 (26) Overshot
000010001110 -> 28 (26) Overshot
100000001110 -> 27 (26) Overshot
xxxxxxxx0110 -> 46 (26)
000000010110 -> 24 (26)
000000110110 -> 28 (26) Overshot
000010010110 -> 27 (26) Overshot
100000010110 -> 26 (26) Match!
xxxxx0000110 -> 34 (26)
000010000110 -> 23 (26)
000110000110 -> 26 (26) Match!
100010000110 -> 25 (26)
x00000000110 -> 22 (26) Undershot
xxxxxxxxx010 -> 41 (26)
000000001010 -> 15 (26)
000000011010 -> 19 (26)
000000111010 -> 23 (26)
000001111010 -> 27 (26) Overshot
000010111010 -> 26 (26) Match!
100000111010 -> 25 (26)
xxxxx0011010 -> 33 (26)
000010011010 -> 22 (26)
000110011010 -> 25 (26)
001110011010 -> 28 (26) Overshot
100110011010 -> 27 (26) Overshot
x00010011010 -> 24 (26) Undershot
x00000011010 -> 21 (26) Undershot
xxxxx0001010 -> 29 (26)
000010001010 -> 18 (26)
000110001010 -> 21 (26)
001110001010 -> 24 (26)
011110001010 -> 27 (26) Overshot
101110001010 -> 26 (26) Match!
x00110001010 -> 23 (26) Undershot
x00010001010 -> 20 (26) Undershot
x00000001010 -> 17 (26) Undershot
xxxxxxxx0010 -> 36 (26)
000000010010 -> 14 (26)
000000110010 -> 18 (26)
000001110010 -> 22 (26)
000011110010 -> 25 (26)
000111110010 -> 28 (26) Overshot
100011110010 -> 27 (26) Overshot
x00001110010 -> 24 (26) Undershot
xxxxx0110010 -> 32 (26)
000010110010 -> 21 (26)
000110110010 -> 24 (26)
001110110010 -> 27 (26) Overshot
100110110010 -> 26 (26) Match!
x00010110010 -> 23 (26) Undershot
x00000110010 -> 20 (26) Undershot
xxxxx0010010 -> 28 (26)
000010010010 -> 17 (26)
000110010010 -> 20 (26)
001110010010 -> 23 (26)
011110010010 -> 26 (26) Match!
101110010010 -> 25 (26)
x00110010010 -> 22 (26) Undershot
x00010010010 -> 19 (26) Undershot
x00000010010 -> 16 (26) Undershot
xxxxx0000010 -> 24 (26) Undershot
xxxxxxxxx000 -> 31 (26)
000000001000 -> 5 (26)
000000011000 -> 9 (26)
000000111000 -> 13 (26)
000001111000 -> 17 (26)
000011111000 -> 20 (26)
000111111000 -> 23 (26)
001111111000 -> 26 (26) Match!
100111111000 -> 25 (26)
x00011111000 -> 22 (26) Undershot
x00001111000 -> 19 (26) Undershot
xxxxx0111000 -> 27 (26)
000010111000 -> 16 (26)
000110111000 -> 19 (26)
001110111000 -> 22 (26)
011110111000 -> 25 (26)
111110111000 -> 27 (26) Overshot
x01110111000 -> 24 (26) Undershot
x00110111000 -> 21 (26) Undershot
x00010111000 -> 18 (26) Undershot
x00000111000 -> 15 (26) Undershot
xxxxx0011000 -> 23 (26) Undershot
xxxxx0001000 -> 19 (26) Undershot
xxxxxxxx0000 -> 26 (26) Match!
000000000000 -> 0 (26) End
Subsets found: 10
Itrations made: 102
Subsets total number: 480
-- 01.02.2018, 13:42 --После недолётной комбинации появляется ещё меньшая. Ну, между ними есть и перелётные комбинации, так что я бы не сказал, что эти две вообще хоть как-то связаны. Даже больше, первая принадлежит той половине комбинаций, в которую входит последний элемент, а вторая — в которую не входит. И кроме как поддержание интересного разговора никаких целей не преследую На самом деле для меня и это очень важно. Собеседник, который не понимает в вопросе, порой может оказаться лучше любого Знайки, потому что когда пытаешь объяснить в подробностях что и зачем делаешь, то во-первых сам начинаешь лучше понимать, что же именно делаешь, а во-вторых, часто бывает так, что замечаешь какую-то какую-нибудь мелкую ошибку или ВНЕЗАПНО приходит озарение, как сделать ещё лучше. Ну и разговор может быть просто стимулом двигаться дальше. Алсо, написание этого алгоритма вызывает у меня жуткое чувство, что я создаю программу для какого-нибудь брэйнфака или другого языка Тьюринговой трясины. -- 01.02.2018, 13:45 --Теперь надо бы создать отдельный функциональный класс, который решает поставленную задачу без всяких статистик и использовать его для по-настоящему жёсткого теста алгоритма.
|

 подмножеств, а
подмножеств, а  узлов. Это было бы хуже. Однако это позволяет по-другому смотреть на проектируемые алгоритм и код и видеть там другие, скажем даже, точки вставки, вообще деление на блоки и потенциальные рефакторинги. Хотя я писал сразу с учётом оптимизаций-отсечений и оптимизации представления узла — никакого дерева там не появляется, массив да индекс.
узлов. Это было бы хуже. Однако это позволяет по-другому смотреть на проектируемые алгоритм и код и видеть там другие, скажем даже, точки вставки, вообще деление на блоки и потенциальные рефакторинги. Хотя я писал сразу с учётом оптимизаций-отсечений и оптимизации представления узла — никакого дерева там не появляется, массив да индекс.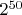 комбинаций, который при производительности
комбинаций, который при производительности  комбинаций в секунду занял бы более 3,5 лет. Не уверен, правда, что тормознутая Джава осилит такую производительность. В общем, не смотря на экспоненциальную по количеству элементов сложность задачи, скорость работы вполне на уровне. Я думаю даже, сложность линейна по количеству существующих комбинаций (но не уверен в этом).
комбинаций в секунду занял бы более 3,5 лет. Не уверен, правда, что тормознутая Джава осилит такую производительность. В общем, не смотря на экспоненциальную по количеству элементов сложность задачи, скорость работы вполне на уровне. Я думаю даже, сложность линейна по количеству существующих комбинаций (но не уверен в этом).