Диффузия с "ограниченной скоростью"

[Ms-dos4]

Возникла тут следующая задачка в связи с достаточно известной темой. Пусть у нас есть частица, которая движется по оси только с двумя скоростями, $ - v$ и $v$. В начальный момент времени частица находится в точке $x = 0$ и с вероятностью 1/2 приобретает скорость $ - v$, с вероятностью 1/2 скорость $v$ (тут конечно задачу можно обобщать, делая несимметричной, но оставим пока так). Далее двигаясь некоторое время $\tau $ (которое, допустим, распределено экспоненциально $\beta {e^{ - \beta \tau }}$) и испытывает рассеяние, в котором приобретает новую скорость аналогично началу её движения. В общем то в такой постановке задача хорошо известна (её исследовал ещё Фок) и приводит к следующему (телеграфному) уравнению на плотность распределения частицы

$$\frac{{{\partial ^2}p}}{{\partial {t^2}}} + 2\beta \frac{{\partial p}}{{\partial t}} = {v^2}\frac{{{\partial ^2}p}}{{\partial {x^2}}}$$

Уравнение может быть точно решено (ответ записывается через модифицированные функции Бесселя первого рода) и характерной особенностью является зануление за "световым" конусом $x > vt$.

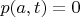
Однако меня интересует немного другой аспект, а именно помещение в исходную задачу поглощающего барьера в точке $x = a$ и вычисления плотности распределения времён первого достижения. Я думал, что достаточно как и в случае обычной диффузии потребовать $p(a,t) = 0$ (в таком случае решение находится методом продолжения н.у.) но вот монте-карловские симуляции этого не подтверждают, распределения получаются другие (хотя тут есть свои вопросы, например переход в Леви-Смирнова какой-то уж слишком плохой в симуляции, тогда как распределение времён первого достижения телеграфного например уже при $a = 10$ и $v = \sqrt \beta = 10$ 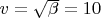трудно отличить от него). В общем мне непонятно, дело ли в кривых граничных для телеграфного уравнения или в случае, когда мы имеем барьер оно принципиально неприменимо? (Попытка честно вывести уравнение начиная с интегральных как в случае без барьера закончилась провалом для меня )

[Vince Diesel]

Я не все понял во втором абзаце, но это же гиперболическое уравнение, а не параболическое. Если закрепить конец струны в точке $a$, то волна, дойдя до нее, отразится а не поглотится. В отличие от уравнения теплопроводности, где тепло будет уходить через конец с условием $p(a,t)=0$.

[Ms-dos4]

Vince Diesel
Да, это верно, спасибо. Но вопрос то какое тогда ставить? Причём ведь уравнение при $v \to \infty $, $\beta \to \infty $ так, чтобы $\frac{{{v^2}}}{{2\beta }} \to D$ переходит в обычную диффузию с коэф. диффузии $D$, и по идее мы должны как то восстанавливать граничное условие $p(a,t) = 0$.
С другой стороны, повторюсь, в непосредственной симуляции блужданий я не вижу перехода в плотность Леви-Смирнова для времён первого достижения - например при $v = \sqrt \beta = 20$ и $a = 10$ распределение полученное симуляциями сильно отличается от плотности $f = \frac{{10}}{{\sqrt {2\pi {t^{3/2}}} }}{e^{ - \frac{{50}}{t}}}$ хотя решение гиперболического уравнения (без барьера) уже практически не отличается от решения диффузионного. Вот и вопрос - возможно при введении поглощающего барьера телеграфное уравнение вообще перестаёт описывать плотность распределения частицы? Я уже совсем запутался здесь...

[amon]

Может ерунду ляпну. Поглощению соответствует предел $\beta\to\infty,$ и мне кажется, что этому соответствует условие $\frac{{\partial p}}{{\partial t}} = 0.$

[Ms-dos4]

amon
Простите, я логику не очень понял. Поглощающий барьер (поглощение в точке $x = a$) есть хоть при каком значении $\beta $, которое характеризует просто время/длину пробега до рассеяния. А при определённом устремлении этого параметра и скорости к бесконечности (писал выше), мы просто переходим от "кинетической" диффузии, у которой ограничена "скорость" к самой обыкновенной

[amon]

Ms-dos4 в сообщении #1284486 писал(а):

Простите, я логику не очень понял.

Положив $\beta=\infty$ при $x\ge a$ получим поглощение в этой точке и дальше ($v$ не трогаем). Это даст условие $\left.\frac{{\partial p}}{{\partial t}}\right|_{x=a} = 0.$ Вроде бы - так...

[пианист]

М.б., будет полезно.
Похожей задачей, гиперболическая теплопроводность, применительно к плазме занимался Е.Н.Сотский.
Еще про гиперболическую теплопроводность написано в книжечке Подстригач, Коляно, Обобщенная термомеханика.

[Vince Diesel]

Для гиперболических уравнений есть интеграл энергии. Насколько помню, уравнение умножается на $p_t$, потом интегрируется по отрезку и времени, затем интегрирование по частям... Для волнового уравнения энергия сохраняется. Можно попробовать посмотреть, что будет для этого (при нулевых граничных условиях). Если сохраняется, то ничего не утекает. Если уменьшается со временем, то как, в зависимости от параметров.

[Ms-dos4]

amon,Vince Diesel,пианист спасибо за советы, посмотрю обязательно.
Мне на кафедре ещё подсказали, что хороший вариант - вернуться к отдельным плотностям частиц, движущихся налево и направо (собственно гиперболическое и выводится из них, где $p = {p_L} + {p_R}$), и на барьере положить равенство плотности нулю для вторых. Это приводит к граничному условию для полной плотности

$$p(a,t) + \frac{v}{{2\beta }}{\left. {\frac{{\partial p}}{{\partial x}}} \right|_{x = a}} + \frac{1}{{2\beta }}{\left. {\frac{{\partial p}}{{\partial t}}} \right|_{x = a}} = 0$$

Видно, что в пределе обычной диффузии восстанавливаем нужное $p(a,t) = 0$. Попробую ещё это путь. Ну и плюс кажется придумал идею, как вычислить распределение времён первого достижения данного блуждания вообще без дифференциальных уравнений, но там свои сложности.