NNDeazТут, мне кажется, та же проблема, что уже была в одной из Ваших прошлых тем. Понимаете ли, в любом тексте есть те или иные условности речи, иначе его ни написать, ни прочитать будет невозможно.
Следует оговориться, что бывают тексты вообще без условностей. А именно, это тексты на строго формализованных языках описания доказательств, таких как Coq. Но они предназначены для другого, а именно, для формальной проверки правильности доказательств компьютером. Компьютер их читать может, а человек --- практически нет. Тем более студент 1 курса. Я в этих формализованных языках не разбираюсь, поэтому больше ничего написать не могу.
Для разных категорий читателей тексты пишутся разного стиля, по определению. Для широкой публики одни, для студентов другие, для профессионалов третьи, для компьютера четвертые. В одних текстах одни условности, в других другие. То, что одно и то же выражение может обозначать разные объекты --- это очень широко распространенный прием, часто облегчающий понимание (а может и наоборот затруднять, в зависимости от ситуации). Иногда разные вещи нужно обозначить одной буквой, иногда можно, иногда нельзя. В данном случае --- вполне уместно (и вообще Кострикин --- отличный учебник, хоть и не все в нем хорошо). Привыкайте.

, где

--- коммутативное кольцо, обозначает множество всех

матриц

, для которых существует матрица

такая, что
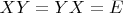
. Легко видеть, что это группа. Отметим, что матрица с элементами из

может иметь ненулевой определитель и тем самым быть обратимой над полем частных кольца

, не будучи обратимой над

.
Наконец, еще такая мысль есть. По моему, интересней гораздо заниматься математикой, а не обращать слишком много внимания на языковые затруднения (тем более если Вы вполне понимаете о чем речь, значит и языковой проблемы-то фактически нет). Вот у Вас недавно была тема про коммутативность некоей системы с бинарным умножением, так с точки зрения любопытства, дорешали Вы ту задачу или нет?