Доброе время суток уважаемые форумчане!
Хотел Вам изложить предмет своих мытарств.. и спросить совет, способ, решение их. Пишу именно в этом разделе потому как ответ на заданный мной вопрос лежит именно в области математической статистики. Сам вопрос будет в конце…, после изложения самой проблематики.
Вначале приведем алгоритм дифференциального кодирования, а затем место, которое возможно изменить для того, что можно было его усовершенствовать.
КОДИРОВАНИЕ Передаваемые биты

(01101001010110011010101 – к примеру), при

, подаются на вход передатчика. В передатчике применяется модуляция М-PSK (фазовая модуляция) со следующим созвездием сигналов:

при

.

Где

–

-й сигнал созвездия модуляции;

– количество сигналов созвездия (может принимать значения 2, 4, 8, 16, 32 … и т.д.);

– число передающих антенн (может принимать значения 1, 2, 4, 8, … и т.д.).
К примеру, если

и

, то

принимает значения

, а если

и

, то

принимает значения

.
Последовательность передаваемых бит

разбивается на группы по

бит

, которые преобразуется в сигналы созвездия модуляции М-PSK. К примеру,

или

.
В случае

(две передающие антенны), кодирование основано на комплексной ортогональной форме и осуществляется по приведенной ниже табл. 1:
 Пояснения к Таблице 1:
Пояснения к Таблице 1:Сигналы

и

являются опорными и передаются первой и второй антенной в момент времени

, а сигналы

и

в момент

(

означает комплексное сопряжение к

). Переданная таким образом матрица

не несет никакой информации о передаваемых данных, является опорной и одновременно комплексной ортогональной формой

(

- эрмитово сопряжение).
В момент времени

в кодер поступает блок информационных бит

, исходя из значений которых по таблице состояний кодера (приведена далее) определяются два комплексных дифференциальных коэффициента

и

, после чего рассчитываются значения сигналов

и

:

.

Выражение (2) называется правилом дифференциального кодирования. Процедура кодирования состоит в вычислении набора коэффициентов

и

по таблице состояний кодера (
число состояний 
), значения которых зависят от множества комбинаций двоичных входных информационных значений

(0 или 1), числа передающих антенн и вида модуляции. Векторы

при каждом из значений

образуют множество

.
В момент времени

через первую и вторую антенны передаются сигналы

и

соответственно, а в момент

– сигналы

и

. Сигнальная матрица

несет информацию блока информационных бит

и также является комплексной ортогональной формой

.
Пример: Таблица состояний кодера при

и модуляции BPSK

(табл. 2)

Аналогичным образом таблица дополнится случаями, при которых значения

и

равны

,

и

,

соответственно.
Таким образом, существует взаимно однозначное соответствие между опорной матрицей

, блоком информационных бит

, дифференциальными коэффициентами

,

и сигнальной матрицей

.
Дифференциальные коэффициенты

и

рассчитываются как

;

и задают множество

до начала процесса кодирования, исходя из возможных значений сигналов

,

,

и

.
Структурная схема кодера передатчика приведена на рисунке.
 ДЕКОДИРОВАНИЕ
ДЕКОДИРОВАНИЕРассмотрим случай использования двух передающих антенн

и одной приемной

. Обозначим через

принимаемый сигнал,

– шум в момент времени

, а

и

– канальные коэффициенты от первой и второй передающей антенны к приемной антенне (используется рэлеевский канал замираний, который поддерживается постоянным лишь (значения

и

– случайные величины) в пределах передачи минимум двух соседних матриц

- условие данного дифференциального метода кодирования). Принятые сигналы в моменты времени

,

,

и

могут быть соответственно записаны:




Дифференциальный коэффициент

(

- обозначает восстановленное значение) определяется

, а коэффициент

.
Приемник путем оценки
максимального правдоподобия (9) выбирает ближайший вектор

из множества парных значений векторов дифференциальных коэффициентов

при каждом из значений

множества

. Затем для декодирования передаваемого блока битов

по Таблице состояний кодера применяется обратное отображение:


где

- норма Фробениуса. То есть,
хочу подчеркнуть, необходимо перебрать
всё множество парных значений векторов дифференциальных коэффициентов

и, соответственно, получим

значений аргумента (вначале вычисляем разность, потом берем норму Фробениуса и так

раз). Затем находим минимальное значение аргумента и смотрим какому значению

оно соответствует. После чего, по Таблице состояний кодера принимаем решение о передаваемых битах

.
При увеличении позиционности фазовой модуляции (при

и т.д.) такой метод (метод максимального правдоподобия) приводит к возрастанию вычислительной сложности декодирования, поскольку число состояний таблицы состояний кодера

(к примеру, при

и


, а при

и


) и нужно будет перебрать
все возможные значения для того, чтобы провести декодирование бит

.
А теперь сам
ВОПРОС: Каким образом возможно сделать, что-то применить, чтобы каждый раз
не перебирать все возможные значения парных векторов дифференциальных коэффициентов

.
В целом структурная схема декодера приемника показана на рисунке.
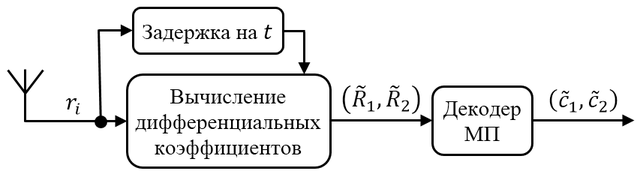
Данный метод дифференциального кодирования основан на принципе относительного кодирования и допускает отсутствие канальной информации на приемной и передающей сторонах.