Пересечение прямых и центр описанной окружности

[alhimikoff]

После проверки через смешанное произведение что они в одной плоскости считаю параметр при котором пересекаются:
Прямые
$ \left\{ \begin{array}{rcl} &x=x_1+A_1t& \\ &y=y_1+B_1t& \\ &z=z_1+C_1t& \\ &x=x_2+A_2t& \\ &y=y_2+B_2t& \\ &z=z_2+C_2t& \\ \end{array} \right. $
Раз прямые пересекаются, их проекции на любую плоскость тоже пересекаются. Выберем плоскость, в которой они не совпадают, например $xy$ и из ур-й 1,2,4 находим $x,y,t$, подставляем в ур-е 3 и находим $z$.

Ищу центр окружности, описанной около треугольника $ABC$
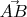
Складываю нормированные вектора $\vec{AB}$ и $\vec{AC}$ - получаю направляющий вектор биссектрисы угла $A$.
Тоже самое для угла $B$.
Пересекаю биссектрисы описанным выше алгоритмом в точке $O$.
Радиусы $OA,OB,OC$ выходят разные! Отличаются примерно на $1/10$. Где ошибка - в пересечении прямых или в поиске центра? Как улучшить точность?

[svv]

alhimikoff в сообщении #1278915 писал(а):

считаю параметр при котором пересекаются

Тут такая штука возможна. Прямые $\mathbf r(t)=\mathbf r_1+\mathbf v_1 t$ и $\mathbf r(t)=\mathbf r_2+\mathbf v_2 t$ пересекаются, но точку пересечения $\mathbf R$ каждая из них проходит при своём значении параметра:
$\mathbf R=\mathbf r_1+\mathbf v_1 t_1=\mathbf r_2+\mathbf v_2 t_2$
И это (в случае, если прямые вообще пересекаются) — ситуация общего положения.

Кинематическая трактовка: два тела, движущиеся равномерно и прямолинейно, прошли через одну и ту же точку в разное время (как чаще всего и будет).

[alhimikoff]

svv
Параметры разные, для одной $t_1$, для второй $t_2$.
Нахожу для одной прямой параметр, и из её же уравнения недостающую координату.
На экране и не видно ошибки в точке, а на окружности вылезает.

[svv]

И значения у них разные в точке пересечения?
И из цитаты, что я привёл, и из записи системы уравнений видно, что Вы ищете общее значение $t$ для обоих параметров.
И даже отсюда:

alhimikoff в сообщении #1278915 писал(а):

находим $x,y,t$

— иначе бы Вы написали $t_1$ или $t_2$.

[alhimikoff]

Ошибся я а поправить не могу. Два разных параметра.

[wrest]

alhimikoff в сообщении #1278915 писал(а):

Ищу центр окружности, описанной около треугольника $ABC$

alhimikoff в сообщении #1278915 писал(а):

Пересекаю биссектрисы описанным выше алгоритмом в точке $O$.

alhimikoff в сообщении #1278915 писал(а):

Радиусы $OA,OB,OC$ выходят разные!

Возможно дело в том, что центром описанной около треугольника окружности является пересечение серединных перпендикуляров, проведенных к сторонам этого треугольника, а не биссектрис его углов.

[alhimikoff]

wrest
Точно, спасибо!