Добрый день. Попалась такая задача:
Цитата:
В треугольнике ABC угол ABC равен 120°. На стороне AC взяты несовпадающие точки M и N так, что

и
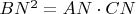
. Радиус окружности описанной около треугольника BMN равен

. Найти AC

Есть только разрозненные мысли, направленные все совершенно в разные стороны:
1. Свойство треугольника с углом 120 градусов, заключающееся в том, что треугольник с вершинами, совпадающими с основаниями биссектрис - прямоугольный как задействовать не вижу, может оно и не нужно.
2. Нашел точки пересечения данной окружности со сторонами AB и BC в точках F и H соответсвенно, нашел по теореме синусов эту сторону:

. Предполагаю, что FH может являться средней линией, и тогда ответ очевиден

. Но может быть это и не так, а если так, то надо доказать.
3. Не дают покоя выражения вида

. Очень похожи на свойство касательной и секущей, но по рисунку ничего похожего не получается. Тогда я попробовал построить на AC как на диаметре полуокружность и провести перпендикуляры из точек M и N. Получил точки

и

соответственно и для них верно, что

и

.
Т.е.
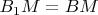
и

.
4. Также, хотел применить теоремы Чевы и Менелая, но не могу найти требуемых конфигураций.
Натолкните пожалуйста на мысль, как пойти с решением дальше. Или, если один из перечисленных пунктов имеет смысл развивать, подскажите хотя бы номер пункта. А также поделитесь пожалуйста ссылкой на материалы по треугольникам 120 градусов. Почему то, кроме свойства биссектрис и точек Ферма-Торричелли более ничего не нашел.
Спасибо, если откликнитесь