Принцип математической индукции. Зорич.

[Ivan_B]

Зорич, стр 53:
"Определение 2. Множеством натуральных чисел называется наименьшее индуктивное множество, содержащее 1, т.е. пересечение всех индуктивных множеств, содержащих число 1."

"b. Принцип математической индукции
Если подмножество $E$ множества натуральных чисел $N$ таково,что $1 \in E$ и вместе с числом $x \in E$ множеству $E$ принадлежит число $x + 1$, то $E =N$."

"$1 \in E$ и вместе с числом $x \in E$ множеству $E$ принадлежит число $x + 1$" означает, что $E$ - индуктивное, включающее 1.
"подмножество $E$ множества натуральных чисел $N$" равносильно "индуктивное подмножество множества натуральных чисел $N$, которое включает $1$"
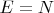
Множество натуральных чисел по определению не содержит собственных индуктивных подмножеств, которые включают 1, поэтому $E=N$ по определению $N$ и $E$.

Контекст, в котором я встречал слова "математическая индукция": Доказать $\sum_{i=1}^n i = \frac{n(n+1)}{2}$ Для $n=1$ формула верна. Пусть формула верна для $n$, тогда для $n+1$ получим $\sum_{i=1}^{n+1} i = \frac{n(n+1)}{2}+(n+1)=\frac{(n+2)(n+1)}{2}=\frac{((n+1)+1)(n+1)}{2}$.

Если я написал бессмыслицу,
Ткните, пожалуйста, пальцем в то, что называется "принципом математической индукции" ($E=N$?).
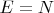
Если ответ не выходит за рамки книги, то
Как доказательство формулы суммы соотносится с определением из Зорича?
Если выходит, подскажите название темы/раздела, в котором это изучается.

[arseniiv]

Соотносится так: пусть $E$ — множество тех натуральных чисел, для которых утверждение

Ivan_B в сообщении #1273718 писал(а):

$\sum_{i=1}^n i = \frac{n(n+1)}{2}$

верно. База индукции эквивалентна утверждению, что в это множество входит 1. Переход эквивалентен тому, что это множество индуктивно. Истинность утверждения для всех $n$ эквивалентно $E = \mathbb N$.

[Ivan_B]

arseniiv в сообщении #1273725 писал(а):

Соотносится так:

Это ответ на мой вопрос и он мне понятен.
Теперь непонятно что это соотношение дает.
Хотелось бы как-то уточнить мое собственное представление: понять что оно неточное, или совсем неверное, или что оно совпадает с тем, что написано в Зориче. Мое представление: если удалось угадать ответ, можно попробовать записать доказательство по "принципу математической индукции". Для этого достаточно установить истинность двух утверждений: базы индукции и индукционного перехода. Этого как бы достаточно, чтобы доказать правильность угаданного ответа. То, что написано в Зориче является обоснованием того, что истинность базы индукции и индукционного перехода влечет истинность утверждения, которое нужно было доказать?

[iifat]

Обоснованием является, вообще говоря, не то, что написано в Зориче или где бы то ни было, а принцип полной математической индукции. И да, принцип полной математической индукции позволяет свести доказательство некоего утверждения к доказательству двух других. Где вы возьмёте изначальное утверждение — математику не интересует. Вы можете угадать, взять подсказку зала, прочитать в учебнике, наконец посадить миллион мартышек колотить по пишущим машинкам...

[SomePupil]

Ivan_B в сообщении #1274293 писал(а):

Мое представление: если удалось угадать ответ, можно попробовать записать доказательство по "принципу математической индукции". Для этого достаточно установить истинность двух утверждений: базы индукции и индукционного перехода.

Хорошее представление.

Ivan_B в сообщении #1274293 писал(а):

То, что написано в Зориче является обоснованием того, что истинность базы индукции и индукционного перехода влечет истинность утверждения, которое нужно было доказать?

Ну, как сказать. Вот это

Ivan_B в сообщении #1273718 писал(а):

Множеством натуральных чисел называется наименьшее индуктивное множество, содержащее 1

является чистой воды определением. Уже на основе такого определения легко обосновать принцип мат. индукции.

[Ivan_B]

Проблем с пониманием написанного в Зориче сейчас у меня нет. Остается ощущение, что что-то не так, но ничего внятного по этому поводу спросить у меня не получается, тем не менее, двигаться дальше это не мешает.
Огромное спасибо Всем за Ваши ответы!