Ну могу отыскать ключик к следующей задаче:
------
Пусть
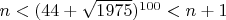
, где

– целое. Докажите, что n — нечетно.
------
Если,

, то
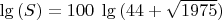
.
С помощью калькулятора находим, что

, остюда

. Осталaсь самая малость: вычислить
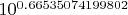
и передвинуть запятую на 194 разряда вправо... Увы, калькулятор способен дать лишь не более 20 значащих цифр, что явно недостаточно для определения четности целой части результата. Я уже не говорю о том, что самым точным вычислительным инструментом, доступным рядовому советскому школьнику в 1975 году были ... математические таблицы Брадиса, дававшие лишь 4 значащие цифры.
Может быть имеет значение тот факт, что
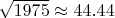
? (Пытался умножить на сопряженное, но помогло.)
-- 03.12.2017, 14:18 --Вот возможный подход:

делится на
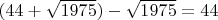
, a

нечетно! Однако это неверно, т.к частное от деления содержит
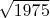
в нечетных степенях, потому не целое.