Аналитическая функция вещественного переменного

[RikkiTan1]

Доброго времени суток!
В книге Г.И. Архипов, В.А. Садовничий, В.Н. Чубариков "Лекции по математическому анализу" есть такая задача.
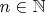
ЗАДАЧА. Пусть $f(x) $ -- бесконечно дифференцируемая на интервале $(a,b)$ функция. Обозначим через $k_n$ число решений уравнения $f^{(n)}(x)=0$. Пусть $k_n<C$ при некотором $C$ и всех $n\in \mathbb{N}$. Доказать, что функция $f(x)$ является аналитической на интервале $(a,b)$.
Опр. Функция $f(x)$ называется аналитической в точке $x_0$, если в некоторой окрестности этой точки она может быть представлена её рядом Тейлора.
Я не знаю, какие следствия можно получить из условия, что количество нулей и самой функции, и любой её производной ограничено одним и тем же числом. Моя основная идея это взять некоторую точку $x_0 \in(a,b)$ и как-нибудь показать, что из того условия следует $f^{(n)}(x_0)\leqslant c^nn!$ для всех $x$ из некоторой окрестности $x_0$.
Подскажите, пожалуйста, какая информация в этом заключена: Пусть $k_n<C$ при некотором $C$ и всех $n\in \mathbb{N}$

[Markiyan Hirnyk]

Задача сформулирована нечетко. Как понимать

Цитата:

Обозначим через $k_n$ число решений уравнения $f^{(n)}(x)=0$

для функции $f(x):=\left \{ \begin{array}{l} e^{\frac {-1}{x^2}},\, x\neq 0;\\0,\,x =0.\\ \end{array} \right . $ при $n=0$ на интервале $(-1,1)?$

[Pphantom]

RikkiTan1 в сообщении #1267683 писал(а):

Я не знаю, какие следствия можно получить из условия, что количество нулей и самой функции, и любой её производной ограничено одним и тем же числом.

Это значит, что оно просто ограничено сверху. На "одном числе" зацикливаться не стоит.

[RikkiTan1]

Markiyan Hirnyk
Наверное, предполагается что $k_n$ - число решений $f^{(n)}(x)=0$ на интервале $(a,b)$. Из этой задачи получается, что для $f(x):=\left \{ \begin{array}{l} e^{\frac {-1}{x^2}},\, x\neq 0;\\0,\,x =0.\\ \end{array} \right . $ в любой окрестности $(-\delta,\delta)$ существует такое $N$, что у $f^{(N)}(x)$ на $(-\delta,\delta)$ нулей больше любого наперед заданного числа.

[Markiyan Hirnyk]

Не понял. У приведенной мною функции (она не аналитическая в точке $x=0$ ни как комлекснозначная функция, ни как действительнозначная функция) единственный нуль на интервале $(-1,1)$ в точке $x=0$. Учтывается ли его кратность? Есла да, то как эту кратность определить? Как отмечено мною, формулировка задачи неаккуратная.

[RikkiTan1]

$f^{(n)}(x)$ - это $n$-ая производная.

[Markiyan Hirnyk]

Не понял вас. Во-первых, согласно общепринятому соглашению, функция является производной нулевого порядка от самой себя. Во-вторых, точка $x=0$ является нулем каждой производной рассматриваемой функции. Учитывается ли его кратность? Если да, то как?

[mihaild]

Вполне понятная формулировка. Существует константа $C$ такая что для любого $n$ мощность множества $\{x | f^{(n)}(x)\}$ не превосходит $C$.
Ваша функция не подходит, потому что число нулей $n$-й производной вашей функции в любой окрестности нуля неограниченно возрастает с ростом $n$.

[Markiyan Hirnyk]

1. Вы также не отвечаете на вопрос о кратности нулей.
2. Пожалуйста, докажите высказанное вами утверждение

Цитата:

Ваша функция не подходит, потому что число нулей $n$-й производной вашей функции в любой окрестности нуля неограниченно возрастает с ростом $n$.

.

[g______d]

Markiyan Hirnyk в сообщении #1268040 писал(а):

1. Вы также не отвечаете на вопрос о кратности нулей.

Нули считаются без учёта кратности. У вашей функции один нуль на интервале $(-1,1)$ при $n=0$. Но из этого, вообще говоря, не следует, что она является контрпримером, потому что в условии задачи число нулей $f^{(n)}$ на отрезке $(a,b)$ должно быть ограничено одной и той же константой при всех $n$, чего вы доказать даже и не пытались.

[Markiyan Hirnyk]

g______d Спасибо за высказанное вами (без аргументации) личное мнение

Цитата:

Нули считаются без учёта кратности.

Если ваше замечание

Цитата:

чего вы доказать даже и не пытались

относится ко мне, то оно верно: я пытаюсь понять и уточнить формулировку задачи, и не более того.

[mihaild]

Markiyan Hirnyk в сообщении #1268056 писал(а):

без аргументации

Приведите определение "решения уравнения", приведите определение "$k_n$ - число решений уравнения $f(x) = 0$" и увидете, что кратность тут вообще не при чем.

[Markiyan Hirnyk]

mihaildДа, действительно, Вики подтверждает эту точку зрения. Однако в комлексном анализе и полиномиальной алгебре кратность нулей существенна и учитывается.

[pogulyat_vyshel]

Хрен с ними с нулями. Имеется гладкая функция на интервале, которая положительна вместе со всеми своими производными. И почему она должна быть аналитичной? Я не знаю :(

[Xaositect]

pogulyat_vyshel
Тут вроде понятно - если $f^{(n)}(0) \geq c$, то $f(x) \geq cx^n/n!$ при $x > 0$, то есть на каждом отрезке можно ограничить производные через разность значений функции на концах.