Это что за чудо-юдо? Откуда оно взялось?
Было получено следующее каноническое ДУ в ЧП:
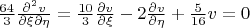
Где

К сожалению, решить в таком виде ДУ сложно, если вообще представляется возможно (по крайней мере мне), и, как написала ув. Lia, необходимо провести замену:

После которой, все первые частные производные уйдут, т.е. получится следующий вид:

Но с ним у меня тоже возникли трудности, которые я никак не могу понять..
Необходимо найти функцию

.
Вообще, Ваше поведение вызывает вопросы, которые отрицательно влияют на желание Вам отвечать.
Прошу прощения, если Вам так показалось.