1) Количество обращений студента в доставку пиццы в течение месяца определяется случайной величиной, принимающей значения

с вероятностями

. Поведение студента в разные месяцы – независимые, одинаково распределенные случайные величины. За один раз заказывается одна пицца.
Выберите верные утверждения (a-d):
a) вероятность ещё ровно одного обращения у студента, обращавшегося уже дважды больше, чем у студента, обращавшегося лишь единожды;
b)
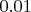
% квантиль суммы заказов двух студентов равна

% квантили суммы заказов трёх студентов;
c) ожидание числа заказов студента по итогам месяца больше ожидания среднего числа заказов студента по итогам года;
d) пусть на второй и третий заказ в течение календарного месяца предоставляется

% скидка; тогда корреляция суммы, потраченной студентом, и числом пицц положительна, но меньше единицы.
Проверим пункт

. Если человек обратился уже дважды в доставку, то вероятность того, что он обратится еще раз будет считаться по формуле.

, где

-- событие заключающиеся в том, что студент обратился дважды.

.

- событие, заключающиеся в том, что студент обратиться в доставку третий раз.


Если человек обратился единожды. то вероятность того, что он обратится еще раз будет считаться по формуле:

, где

-- событие заключающиеся в том, что студент обратился один раз.

.

- событие, заключающиеся в том, что студент обратиться в доставку во второй раз, но не обратится в третий .


, чего быть не может....
b) Имеется ввиду, что для

и

, при этом

? Но этого думаю, что быть не может, потому как при добавлении к сумме

еще
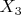
, перцентиль только может уменьшится, но никак не увеличится. Правильно ведь, не может стать уровень

.
c) Мне кажется, что они должны совпадать ожидания и среднее, потому как по смыслу -- это одно и тоже, но тот факт, что разный временной диапазон -- никак не повлияет, потому как у нас случайные величины независимы и одинаково распределены.
d) Думаю, что положительна будет корреляция, потому как, если даже из-за скидки количество заказанных пицц будет больше, то и суммарные деньги, которые за них будут уплачены -- увеличены. Может ли быть корреляция равна 1? Пока не знаю, это ведь будет выполнимо только в случае линейной зависимости, но ведь скидка слегка корректирует зависимость, вряд ли она будет линейной...