Сумма выглядит страшновато...
Не знаю, насколько будут полезны соображения, но они - такие:
1. Суммы такого рода встречаются, когда мы решаем уравнение теплопроводности на отрезке (с нулевыми граничными условиями) методом Фурье. Ну, например, замечательная задача, которую придумал мой друг: показать, что если
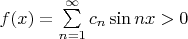
, то и

. Решение: вторая сумма - это решение ур. тепл-ти на
![$[0,\pi]$ $[0,\pi]$](https://dxdy-03.korotkov.co.uk/f/2/3/8/2385bc03c71e0b4fd8db3bac2e36c7f282.png)
(с начальным условием

, и граничными нулями ) в момент

. По принципу максимума, оно больше нуля.
Смущает, однако, множитель
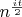
. Мне бы больше понравился

- чтоб было похоже на ряд Фурье....
2. Можно попробовать интерпретировать Ваше произведение как характеристическую функцию некоторого распределения (характеристическая функция суммы независимых случайных равна произведению хар. ф-й) в некоторой точке. Да и слагаемые в сумме похожи на хар функции нормального распределения...
Но конкретно - не вижу, как сделать задачку. А опечаток точно нет?