Задача по планиметрии

[Ironclad]

Добрый день!

На рисунке $AB$, $CD$, $KE$ - касательные к окружности, причём $AB$ параллельна $CD$. Докажите, что угол $KOE$ равен $90^o$.


Понятно, что сумма внутренних односторонних углов равна $180^o$, т. е. $AKE+CEK=$$180^o$
Угол $KOE=180^o-OKE-OEK=180^o-AKO-CEO$
Если провести к точкам касания прямых $AB$ и $CD$ с окружностью радиусы в точки $X, Y$, получим два прямоугольных треугольника. Тогда можно выразить угол $KOE$ так:
$KOE=180^o-XOK-YOK=180^o-90^o+AKO-90^o+CEO=AKO+CEO$
Таким образом, $AKO+CEO=180^o-AKO-CEO$

Но всё это пока не приблизило меня к доказательству... Что ещё мне следует учесть?

[VAL]

Провели две касательных к окружности из одной точки. А затем ту же точку соединили с центром. Чем является третья прямая по отношению к первым двум?

[INGELRII]

Я бы провел еще одну касательную параллельно $KE$ и взглянул на получившийся четырехугольник.

[fred1996]

Ironclad
У вас уже проведено все что надо.
Прямая $OK$ выходит из угла $AKE$
Как она называется по отношению к этому углу?

[Ironclad]

Благодарю всех за ответы.

VAL в сообщении #1258648 писал(а):

Провели две касательных к окружности из одной точки. А затем ту же точку соединили с центром. Чем является третья прямая по отношению к первым двум?

Биссектрисой угла, который они образуют...

fred1996 в сообщении #1258658 писал(а):

Прямая $OK$ выходит из угла $AKE$
Как она называется по отношению к этому углу?

Биссектриса. В равнобедренном треугольнике она является также высотой, что позволило бы доказать, что угол $KOE$ - прямой. Но как доказать, что треугольник $AKE$ - равнобедренный? Если бы его стороны $AK$ и $KE$ были заключены между точкой $K$ и точками касания, было бы ясно...

INGELRII в сообщении #1258649 писал(а):

Я бы провел еще одну касательную параллельно $KE$ и взглянул на получившийся четырехугольник.

Спасибо. Так тоже можно, но хотелось бы, по возможности, решить без четырёхугольников. :)

-- 24.10.2017, 23:56 --

Ironclad в сообщении #1258741 писал(а):

Но как доказать, что треугольник $AKE$ - равнобедренный?

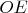
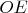
Теперь понял, как доказать это. :) Используя равенство внутренних накрест лежащих углов при прямых $AB$ и $CD$ и секущей $OE$, а следовательно - равенство углов при основании треугольника $AKE$, т. к. $OE$ - также биссектриса угла $CEK$.
Большое спасибо всем за помощь.

[Someone]

Ironclad в сообщении #1258741 писал(а):

Но как доказать, что треугольник $AKE$ - равнобедренный?

Никак, потому что точка $A$ — не фиксированная.

Ironclad в сообщении #1258647 писал(а):

Понятно, что сумма внутренних односторонних углов равна $180^o$, т. е. $AKE+CEK=$$180^o$

Ironclad в сообщении #1258741 писал(а):

Биссектрисой угла, который они образуют...

Это — всё, что требуется. После этого $\angle KOE$ вычисляется мгновенно.

[Ironclad]

Someone в сообщении #1258746 писал(а):

Никак, потому что точка $A$ — не фиксированная.

Пардон. Я её мысленно зафиксировал в точке пересечения прямой $AB$ с прямой, содержащей отрезок $OE$.

Цитата:

Это — всё, что требуется. После этого $\angle KOE$ вычисляется мгновенно.

Точно. Теперь до меня дошло и это. Спасибо.