Задача про лазер

[guitar15]

С какого расстояния $r$ можно увидеть невооруженным глазом свет лазера, генерирующего в непрерывном режиме $P = 10$ кВт на частоте $\omega= 4 \cdot10^{15} c^{-1}$, если для формирования луча используется параболическое зеркало с диаметром $D = 5$ м? Глаз видит источник, если в зрачок диаметром $d =$5 мм попадает в 1 с $n = $60 квантов излучения, лежащего в зеленой части спектра.
Моя попытка решения:
Расстояние, которое проходит лазер определяется по формуле:

$$ r=c\Delta t$$

где $\Delta t$- время за которое лазер проходит расстояние $r$
Мощность излучения

$$ P=\frac{NE}{\Delta t}$$

где, N- количество частиц с генерируемая зеркалом ($\frac N n= \frac D d$, где $n$ -количество частиц попадающих в глаз). После подстановки всех формул получим:

$$ r=\frac{n D\nu h}{dP}$$

Но в ответе:

$$r=\frac{Dd}{2}\sqrt{\frac{D}{h c\lambda n}}$$

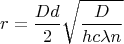
Почему? Что я здесь не учел?

[Xey]

Излучаемые фотоны распределяется по кругу , диаметр которого определяется углом дифракции на зеркале и расстоянием

[guitar15]

В данном случае у нас дифракция Фраунгофера?

-- 01.05.2017, 14:14 --

Цитата:

диаметр которого определяется углом дифракции на зеркале и расстоянием

У нас зеркало создает дифракцию? Непонятно, что за угол?

[Xey]

Дифракция на щели , на отверстии.

[guitar15]

Но отверстии зрачка глаза. Правильно?
Если да, на зрачок падают параллельные лучи?

[Xey]

Диаметр зеркала , это диаметр отверстия.

[guitar15]

В нашем случае круглое отверстие поэтому угол дифракции определяется по формуле

$$\sin \varphi =1,22 \frac \lambda D $$

Я прав?

-- 01.05.2017, 15:28 --

Если найдем $\varphi$, то найдем расстояние до глаза. Не понятно как влияет на ситуацию диаметр зрачка глаза?

[se-sss]

guitar15 в сообщении #1213399 писал(а):

$\frac N n= \frac D d$

Число частиц пропорционально площади же. Если я правильно понял обозначения, то справа ${(\frac D d)}^2$.

И ещё одно. Дифракция здесь заключается не в том, что происходит в глазе, а в том, что изначально параллельный пучок не может продолжать двигаться параллельно.
И угол расхождения пучка $\sim\frac{\lambda}{D}$. Причём нет резкой границы пучок - не пучок. Но в рамках этой задачи конус - хорошее приближение.
Представьте себе узкий канал, который выходит в море. По каналу идёт волна (параллельный пучок, ограниченный каналом). Волна выходит в море и там она продолжит движение, но будет "размываться".

[Xey]

Найдёте расстояние , на котором диаметр луча станет таким, что в глаз за секунду попадет нужное число фотонов

Забыл отправить , кажется не поздно

[guitar15]

Используя формулу которую я написал сверху получается

$$\sin \varphi =\frac{D}{\sqrt{D^2+r^2}}=1,22 \frac \lambda D$$

Тогда

$$r=D\sqrt{\left(\frac{D}{1,22\lambda}\right)^2+1}$$

[DimaM]

guitar15 в сообщении #1213466 писал(а):

Используя формулу которую я написал сверху получается

$$\sin \varphi =\frac{D}{\sqrt{D^2+r^2}}=1,22 \frac \lambda D$$

А какой вы смысл вкладываете в эту формулу?

Лучше идите с конца: определите, при какой удельной мощности в глаз попадает требуемое количество фотонов в секунду, затем найдите, какой при этом будет диаметр луча, и дальше через угол расхождения определите требуемое расстояние.

[guitar15]

У меня получилось так:
Пусть мощность на зрачке глаза равна $P=NP_0=Nh\nu$.
Удельная мощность равна $k=\frac{4P_0 n}{\pi d^2}$, или $\frac{4P}{\piA^2}=\frac{4P_0 n}{\pi d^2}$, где $A$ - диаметр зрачка.
После преобразования получим:
$A=d\sqrt{\frac{P}{\nu h n}}$
Угол расхождения определяется как
$\varphi= 1,22\frac \lambda D= \frac{A}{2r}$
Получим
$r=\frac{Dd}{2}\sqrt{\frac{P}{cn\lambda}}$
Верно ?

[DimaM]

guitar15 в сообщении #1213472 писал(а):

где $A$ - диаметр зрачка.

Так диаметр зрачка $d$. Может, имеется в виду диаметр луча?

-- 01.05.2017, 22:31 --

guitar15 в сообщении #1213472 писал(а):

Верно ?

Постоянная Планка где-то потерялась.

[guitar15]

Я забыл написать
$\frac{4P}{A^2\pi}=\frac{4P_0 n}{\pi d^2}$,

-- 01.05.2017, 19:33 --

$r=\frac{Dd}{2}\sqrt{\frac{P}{cnh\lambda}}$

-- 01.05.2017, 19:34 --

Верно?

-- 01.05.2017, 19:52 --

Я здесь не учитываю 1,22 .Так можно?

[DimaM]

guitar15 в сообщении #1213485 писал(а):

Я здесь не учитываю 1,22 .Так можно?

Можно, я думаю.