Предел интегрирования внутри интеграла

[SomePupil]

Пусть $f $ везде непрерывна. Надо доказать, что

$$\int\limits_{0}^{x}f(t)(x-t)dt = \int\limits_{0}^{x}\left(\int\limits_{0}^{t}f(u)du\right)dt.$$

Я решил вот так. Пусть

$$F(x) = \int\limits_{0}^{x}f(u)du.$$

Интегрируя по частям исходное выражение, получаем:

$$\int\limits_{0}^{x}f(t)(x-t)dt = F(t)(x-t)\bigg|_0^x + \int\limits_{0}^x F(t)dt = \int\limits_{0}^x F(t)dt = \int\limits_{0}^{x}\left(\int\limits_{0}^{t}f(u)du\right)dt.$$

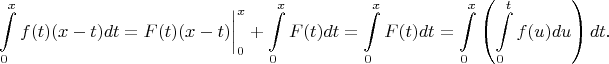
Что и требовалось.

Можно ли так делать? Я убедил себя, что можно, так как я фиксирую $x.$ То есть, переменная как бы застывает во время интегрирования, а затем снова оживает. Это законно?

[demolishka]

Если сомневаетесь, подставьте вместо $x$ конкретные числа. Сначала, например, $1$, потом $\frac{1}{2}$, потом $e$, $\pi$ и продолжайте, пока не перестанете сомневаться

[Dan B-Yallay]

demolishka в сообщении #1207560 писал(а):

Если сомневаетесь, подставьте вместо $x$ конкретные числа. Сначала, например, $1$, потом $\frac{1}{2}$, потом $e$, $\pi$ и продолжайте, пока не перестанете сомневаться

Интересное предложение - проверить перебором.
А если я очень сомнительный - проверять континуум вариантов? Или только все рациональные числа и продолжить по непрерывности?

[demolishka]

Dan B-Yallay в сообщении #1207563 писал(а):

Интересное предложение - проверить перебором.

Я и не предлагал проверять перебором. Я подвел к тому, что от того написано там конкретное число или произвольное (которое и обозначено за $x$) суть дела не меняется.

SomePupil в сообщении #1207553 писал(а):

Я убедил себя, что можно, так как я фиксирую $x$. То есть, переменная как бы застывает во время интегрирования, а затем снова оживает.

Ну фиксировано $x$ или переменно, что с того? Написанные равенства от этого не перестают быть верными.

[Dan B-Yallay]

demolishka в сообщении #1207567 писал(а):

Я и не предлагал проверять перебором

Тогда это я просто неправильно понял. С Вашими доводами согласен.