Задача: Брусок массой

кг, образующий с горизонтом угол
![$\[\alpha \]$ $\[\alpha \]$](https://dxdy-03.korotkov.co.uk/f/a/0/b/a0b2054e7bad2f2818e3ff801fa7a41882.png)
(
![$\[\sin \alpha = 0.6\]$ $\[\sin \alpha = 0.6\]$](https://dxdy-02.korotkov.co.uk/f/d/0/3/d034e13fba6bcbebaeac28f8ed1bdd1e82.png)
).Брусок соединен с вершиной наклонной плоскости недеформированной пружиной жесткостью

Н/м. Какую скорость

нужно сообщить бруску вверх вдоль наклонной плоскости, чтобы он вернулся и остановился в начальной точке? Коэфф. трения равен

.
Решение:
Рассмотрим первый случай, когда тело "пнули" вверх и оно замерло в высшей точке.
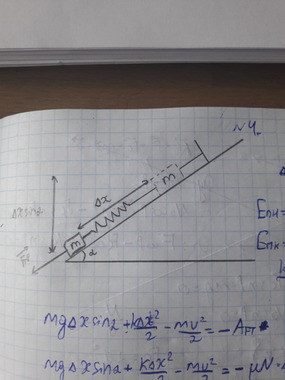
![$$\[\begin{gathered}
\vartriangle {E_0} = - {A_{{F_\mu }}} \hfill \\
mg\vartriangle x\sin \alpha + \frac{{k\vartriangle {x^2}}}{2} - \frac{{m{v^2}}}{2} = - \mu mg\vartriangle x\sin \alpha \hfill \\
\frac{{m{v^2}}}{2} = \vartriangle x\left( {\mu mg\sin \alpha + \frac{{k\vartriangle x}}{2} + mg\sin \alpha } \right) \hfill(1) \\
\end{gathered} \]$$ $$\[\begin{gathered}
\vartriangle {E_0} = - {A_{{F_\mu }}} \hfill \\
mg\vartriangle x\sin \alpha + \frac{{k\vartriangle {x^2}}}{2} - \frac{{m{v^2}}}{2} = - \mu mg\vartriangle x\sin \alpha \hfill \\
\frac{{m{v^2}}}{2} = \vartriangle x\left( {\mu mg\sin \alpha + \frac{{k\vartriangle x}}{2} + mg\sin \alpha } \right) \hfill(1) \\
\end{gathered} \]$$](https://dxdy-02.korotkov.co.uk/f/d/9/5/d95077182f7626b0fbe08ecf8fc2390282.png)
Теперь рассмотрим случай, когда тело из высшей точки попадает в ту точку, где оно было первоначально.

![$$\[\begin{gathered}
\vartriangle {E_{01}} = mg\vartriangle x\sin \alpha + \frac{{k\vartriangle {x^2}}}{2} \hfill \\
\vartriangle {E_{02}} = 0 \hfill \\
\vartriangle {E_0} = \vartriangle {E_{02}} - \vartriangle {E_{01}} = - mg\vartriangle x\sin \alpha - \frac{{k\vartriangle {x^2}}}{2} \hfill \\
\hfill \\
\vartriangle {E_0} = {A_{{F_\mu }}}^\prime \hfill \\
mg\vartriangle x\sin \alpha + \frac{{k\vartriangle {x^2}}}{2} = \mu mg\sin \alpha \hfill \\
\vartriangle x = \frac{{2mg\sin \alpha (\mu - 1)}}{k} \hfill \\
\end{gathered} \]$$ $$\[\begin{gathered}
\vartriangle {E_{01}} = mg\vartriangle x\sin \alpha + \frac{{k\vartriangle {x^2}}}{2} \hfill \\
\vartriangle {E_{02}} = 0 \hfill \\
\vartriangle {E_0} = \vartriangle {E_{02}} - \vartriangle {E_{01}} = - mg\vartriangle x\sin \alpha - \frac{{k\vartriangle {x^2}}}{2} \hfill \\
\hfill \\
\vartriangle {E_0} = {A_{{F_\mu }}}^\prime \hfill \\
mg\vartriangle x\sin \alpha + \frac{{k\vartriangle {x^2}}}{2} = \mu mg\sin \alpha \hfill \\
\vartriangle x = \frac{{2mg\sin \alpha (\mu - 1)}}{k} \hfill \\
\end{gathered} \]$$](https://dxdy-03.korotkov.co.uk/f/e/d/5/ed51eff7b46f1b25c28a0edbf931fb3082.png)
Подставим
![$\[\vartriangle x\]$ $\[\vartriangle x\]$](https://dxdy-03.korotkov.co.uk/f/2/e/5/2e575ae31e0af08584a64a3f817106e982.png)
в уравнение (1):
![$$\[\begin{gathered}
\frac{{m{v^2}}}{2} = \frac{{2mg\sin \alpha (\mu - 1)}}{k}\left( {\mu mg\sin \alpha + mg\sin \alpha (\mu - 1) + mg\sin \alpha } \right) \hfill \\
\frac{{m{v^2}}}{2} = \frac{{2mg\sin \alpha (\mu - 1)}}{k} \cdot 2\mu mg\sin \alpha \hfill \\
v = 2g\sin \alpha \sqrt {\frac{{2\mu m(\mu - 1)}}{k}} \hfill \\
\end{gathered} \]$$ $$\[\begin{gathered}
\frac{{m{v^2}}}{2} = \frac{{2mg\sin \alpha (\mu - 1)}}{k}\left( {\mu mg\sin \alpha + mg\sin \alpha (\mu - 1) + mg\sin \alpha } \right) \hfill \\
\frac{{m{v^2}}}{2} = \frac{{2mg\sin \alpha (\mu - 1)}}{k} \cdot 2\mu mg\sin \alpha \hfill \\
v = 2g\sin \alpha \sqrt {\frac{{2\mu m(\mu - 1)}}{k}} \hfill \\
\end{gathered} \]$$](https://dxdy-02.korotkov.co.uk/f/d/c/9/dc942d4805f90897988c07fcaaeda73582.png)
Однако, подставляя данные, получается, что подкоренное выражение отрицательно.