Доказать что + функция.

[Maviru]

Определим отношение ~ на

$ A:=\{\,(x,y)\in\mathbb{Z}*\mathbb{Z}: y\neq 0\,\}$

следующим образом:

$(x_1,y_1)\sim(x_2,y_2) $\Leftrightarrow x_1y_2=x_2y_1
В первом пункте задачи надо доказать, что ~ отношение эквивалентности (решено). Обозначим [x,y] класс эквивалентности (х,y) по отношению к ~. Определим

[x,y]+[v,w]:=[xw+vy,yw]

Доказать , что + фунция множеств А/~*A/~ и A/~.

Как это доказать? Как использовать в доказательстве, что [x,y] класс эквивалентности (х,y)?

[Brukvalub]

Нужно проверить, что, хотя операция определена с использованием представителей из классов эквивалентности, на самом деле она не зависит от их выбора во взятых классах.

[Maviru]

Можно ещё подсказку? Я должна взять (x',y')~(x,y) и (v',w')~(v,w) идоказать, что (x'w'+v'y',y'w')=(xw+vy,yw)?

[PAV]

Вы складываете классы, но эта операция основана на произвольном выборе их представителей. Нужно доказать, что от этого выбора результат не изменится. Достаточно это сделать для одного из слагаемых, так как операция симметрична. Т.е. нужно показать, что если две разные пары (x,y) и (x',y') задают один и тот же класс (т.е. эквивалентны), то [x,y]+[v,w] = [x',y']+[v,w] для любого класса [v,w]

[Maviru]

Уменя нет никаких соображений как можно решить такую задачу -
Есть такие определения - класс эквивалентности:
[x,y]:={ (x',y') | (x',y')~(x,y) }

разве неверно утверждение (x',y')~(x,y)$\Leftrightarrow[x,y]=[x',y']?

И определение функции:
R - фунция, если для каждых x,y,y'
$(x,y),(x,y')\in R$\Rightarrow y=y'

Если R - это наш +, то x=?, y=?, y'=?

[незваный гость]

Давайте я попробую переформулировать покороче:

(1) у нас есть некоторое множество $X$ и отношение эквивалентности на нём. Мы определяем множество классов эквивалентности $X^*$ как $\{ \{x' \in X | x' \sim x\} \}$

(2) Мы определили функцию $f: X \to X$ некотором образом. Естественное желание — построить $f^*: X^* \to X^*$ Но для этого надо доказать, что как бы мы не выбрали $x' \sim x$, $f(x) \sim f(x')$.

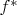
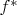
(3) Пример: $X = {\mathbb R} \times {\mathbb R}$, $(x,y) \sim (x',y') \Leftrightarrow $ $x-y = x'-y'$. $f( (x,y) ) = (y, x)$. Проверяем, что $f^*$ функция. Для произвольного $(x', y') \sim (x,y)$ имеем $f((x',y')) = ( y', x')$. Но $f((x,y)) \sim f((x',y')) \Leftrightarrow $ $( y, x) \sim ( y', x')\Leftrightarrow $ $y-x = y'-x'$, что очевидно. Значит, $f^*$ — функция.

Добавлено спустя 4 минуты 18 секунд:

Maviru писал(а):

Есть такие определения - класс эквивалентности:
‹…›
И определение функции:

В этих определениях разные вещи обозначены одной и той же буквой. Строго говоря, там должны стоять кванторы всеобщности, которые свяжут переменные $x, y…$, и которые Вы пропустили.

[Maviru]

Так правильно?
Для произвольного $(x',y') \sim (x,y) \Leftrightarrow x'y=xy' $имеем $f((x',y')+(v,w))=(x'w+vy',y'w). $ Но $f((x',y')+(v,w)) \sim f((x,y)+(v,w))\Leftrightarrow(x'w+vy',y'w)\sim(xw + vy,yw)\Leftrightarrow(x'w +vy')(yw)=(xw+vy)(y'w)\Leftrightarrow x'wyw + vy'yw = xwy'w + vyy'w\Leftrightarrow$ (используем $ x'y=xy')vy'yw=vy'yw.$

И это доказывает, что + функция, т.к. результат не зависит отвыбора представителя класса...

[Brukvalub]

Верно.

[Maviru]

Ура Спасибо всем, кому хватило терпения объяснить и проверить

[незваный гость]

Нет. Во-первых, откуда взялся $f$? Ваша функция обозначена $+$. Во-вторых, Вам надо доказывать более сильное утверждение: $(x',y')+(v',w') \sim (x,y) + (v,w)$.

P.S. Пишите $ вокруг формул. Почитайте введение.

[Brukvalub]

Операция симметрична по аргументам, "снятие" штришков можно производить последовательно, поэтому доказанного достаточно для обоснования полного вывода, иначе получится черезчур громоздко.

[незваный гость]

Brukvalub, я с Вами согласен. Но, мне представляется, Вы смешали статью с учебной задачей. Всё, что сказали Вы, и не сказал Maviru — необходимая часть решения. Да и её нормальный преподаватель попросит расшифровать.

И остался ещё пункт про $f$.

[Brukvalub]

Согласен, просто я привык для себя "проглатывать" такие привычные ходы в рассуждениях

[Maviru]

Полный ответ

$ (v,w)\sim(v',w')\Leftrightarrow vw'=v'w$
$ (x,y)\sim(x',y')\Leftrightarrow xy'=x'y$

$(x',y')+(v',w')=(x'w'+v'y',y'w')$

$(x'w'+v'y',y'w')\sim(xw+vy,yw)\Leftrightarrow ...x'w'yw+v'y'yw = wy'y'w'+vyy'w'$

Последнее равенство верно, т.к.vw'=v'w и xy'=x'y
И это доказывает, что + функция, т.к. результат не зависит от выбора представителя класса...

[незваный гость]

Это уже правильно, но Вы допустили опечатку после стрелки.

Добавлено спустя 1 минуту 1 секунду:

$ ...x'w'yw+v'y'yw = \bold{wy'}y'w'+vyy'w'$

Добавлено спустя 32 секунды:


Боже мой! рациональные числа не узнал