Ранговые корреляции случайных процессов

[Andrey_Kireew]

Экспериментируя с нормальными псевдослучайными векторами (генератор matlab) обнаружил следующую закономерность.
Все парные корреляции компонент векторов, по абсолютной величине, укладываются в диапазон $\Delta R \approx\frac{3}{\sqrt{N-2}}$, т. е. выполняется хорошо известное правило 3-х сигм. Для ранговых корреляций Спирмена и Кендалла наблюдается то же самое, разумеется $\sigma$ у них другие, но правило 3-х сигм выполняется так же хорошо.

После этого я выполняю декоррелирующее преобразование методом главных компонент, обнуляющее все взаимные корреляции Пирсона. Ранговые корреляции при этом не обнуляются, но диапазон их варьирования сужается в 3 раза, т.е. от 3-х сигм до 1 сигмы. Проверялось многократно, получается всегда примерно тоже самое.

Как это можно интерпретировать? Почему ранговые корреляции не обнуляются, ведь насколько я знаю корреляции Спирмена можно вычислять аналогично корреляциям Пирсона, заменив значения на их ранги. И почему диапазон их варьирования уменьшается именно до 1 сигмы, а не до 2-х, например, или до 1,5?

[Евгений Машеров]

Потому, что переход от значений переменной к рангам это нелинейное преобразование. Точное выражение написать затрудняюсь, поскольку ранг элемента зависит не только от его значения, но и от значений всех прочих элементов выборки. А приблизительно ранг будет $R(x_i)=nF(x_i)$ где $F(x)$ функция распределения величины. Нелинейные же преобразования корреляции не сохраняют.

[Евгений Машеров]

А насчёт "отчего 3 сигмы" - а при изменении длин векторов это сохраняется?

[Andrey_Kireew]

да, всегда сохраняется

-- 20.02.2017, 16:07 --

сначала $r_{max}\approx\rho_{max}\approx3\sigma$, потом, после декорреляции по Пирсону $r_{max}\approx0$, а по Спирмену $\rho_{max}\approx \sigma$

-- 20.02.2017, 16:18 --

У меня была идея, что доверительные интервалы корреляций Пирсона и Спирмена расширяются из за уменьшения числа степеней свободы главных компонент по сравнению с исходными сигналами, и расширяются они по разному. Но тогда всё бы зависело от числа компонент и длинны векторов, а здесь примерно всегда одно и то же. После декорреляции ранговые корреляции продолжают распределятся в диапазоне $1\sigma$.

-- 20.02.2017, 16:20 --

причём распределяются они примерно по нормальному закону, что до декорреляции, что после неё.

-- 20.02.2017, 17:00 --

Зато из этого следует полезный вывод: нелинейные преобразования главных компонент изменяют их взаимные корреляции, но они никогда не смогут увеличить эти корреляции более $1\sigma$ (для нормально распределённых величин - можно использовать как критерий нелинейности).
Т. е. различия между корреляциями Пирсона и Спирмена можно рассматривать как своеобразный запас на нелинейные трансформации. Но вот почему именно 1 сигма - это продолжает оставаться загадкой ...

[Евгений Машеров]

Я бы предполагал, что по мере роста длин векторов корреляции Спирмена тоже должны падать. Но, поскольку дисперсия коэффициентов при этом падает, эффект маскируется, и проявился бы при очень сильной разнице длин, в десятки и сотни раз. Впрочем, тут желателен численный эксперимент.
Что же до

Andrey_Kireew в сообщении #1194092 писал(а):

нелинейные преобразования главных компонент изменяют их взаимные корреляции, но они никогда не смогут увеличить эти корреляции более $1\sigma$

то давайте рассмотрим две величины. Одна из них стандартная нормально распределённая $x=N(0,1)$, а вторая
$y=\begin{cases} -x,&\text{если $|x|\le p$;}\\ x,&\text{если $|x|> p$.} \end{cases} $
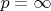
где p - параметр. Очевидно, при $p=0$ корреляция между x и y единица (это две тождественные величины), а при $p=\infty$ минус единица (противоположные), и существует значение p, при котором корреляция x и y нулевая. Соответственно, вычисление ГК для ортогональных величин оставит их неизменными. Но возведём их в достаточно высокую нечётную степень, и получим сколь угодно близкую к единице корреляцию преобразованных величин.
Если вспомнить, что корреляции Спирмена вычисляются по той же формуле, что и Пирсона, только с заменой значений их рангами, взять в качестве рангов их приближения функцией распределения $r_i=nF(x_i)$, а функцию нормального распределения разложить в ряд Тейлора, получим
$\Phi(x)=0.5+I(x)=0.5+\frac 1 {2\pi}\Sigma_{i=0}^\infty \frac {(-1)^nx^{2n+1}}{2^n n!(2n+1) }\approx 0.5+\frac 1 {2\pi}(x-x^3/6+x^5/40+\ldots)$
Постоянный сдвиг и общий сомножитель для корреляции несущественен, член с x в первой степени компенсирован при ортогонализации, а кубический и последующие - нет.

[Andrey_Kireew]

Интересное объяснение

[Евгений Машеров]

Евгений Машеров в сообщении #1193822 писал(а):

А приблизительно ранг будет $R(x_i)=nF(x_i)$ где $F(x)$ функция распределения величины.

Во избежание недоразумений. Имеется в виду "приблизительно", если F(x) это функция распределения, исходя из которой генерировались случайные величины. Если F(x) эмпирическая функция распределения, то формула будет сколь точна, столь бесполезна