Edward_Tur писал(а):
Во-первых, подставляя

, получаем, что

. Подставляя

, получаем, что
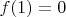
. Подставляя

, получаем, что

.
Пусть теперь

. Тогда

или

. Обозначим

.
Тогда


.(!)
Далее, функция

удовлетворяет следующему функциональному уравнению:

.
Подставим в него

вместо

. Получим (учитывая равенство

):

.
Из этих двух равенств следует:
 = x^2(y^2-\frac{1}{y^2})g(y) - y^2(x^2-\frac{1}{x^2})g(x)$ $[x(y-\frac{1}{y})g(y) - y(x-\frac{1}{x})g(x)](\frac{y}{x} +\frac{x}{y}) = x^2(y^2-\frac{1}{y^2})g(y) - y^2(x^2-\frac{1}{x^2})g(x)$](https://dxdy-03.korotkov.co.uk/f/6/2/e/62e0566db6ad0fe7129dd3bed34bb3c982.png)
или после очевидных преобразований:

Откуда следует, что, при


Значит, при

,

, и

.