Для малого отрезка

с линейным током
 он
он определяется в виде дифференциального соотношения
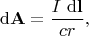
где

-- модуль вектора, проведённого в точку наблюдения из отрезка тока, который наблюдён.
Рассмотрим кольцо с постоянным (в том числе вдоль провода) током

радиуса

. Нужно найти векторный потенциал на оси этого кольца на расстоянии

от его центра. (направление -- пусть туда, куда и

).
Вот я выписываю интегральное соотношение.

где

-- провод. Где моя ошибка?