Добрый день, изучаю сейчас численные методы уравнения Пуассона и никак не могу понять суть многосеточных методов.
Как я вижу, что происходит:
Вот мы имеем систему

для нашего уравнения Пуассона и сетку
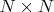
, причём

. Мы делаем первое предположение о решении

, после чего:
1. Делаем одну (можно и больше, наверное) итерацию методом Якоби или Гаусса-Зейделя на исходной сетке

.
2. Вычисляем невязку

.
3. Преобразуем полученную невязку в невязку более грубой сетки с помощью соответствующего оператора

:

4. Решаем уравнение для погрешности

на грубой сетке:

.
5. Преобразуем полученную ошибку на исходную сетку

:

. После чего делаем поправку к нашему решению:

.
6. Повторяем шаг 1.
У меня две основных проблемы. Во-первых, я не до конца осознаю мотивацию (ну, то есть я знаю, что этот метод существенно быстрее методов Якоби или Гаусса-Зейделя, но не очнь понимаю почему). А во-вторых, мне не до конца понятен шаг 4 и сопряжённый с ним V-цикл (или ещё более сложные вещи). То есть обычно пишут, что на шаге 4 нам, по сути, нужно опять решать исходную задачу, хотя и с другой матрицей

, которую можно по-разному аппроксимировать. Поэтому здесь опять можно вызвать алгоритм 1-6. Вопрос, когда остановиться? Мне казалось, что условие остановки процедуры - величина погрешности. Но здесь, видимо, что-то иное имеется в виду (мол, погружаемся всё "ниже и ниже" по разрешению сетки, а потом всплываем). Но мне это как-то не очень понятно. Может ли кто-нибудь совсем на пальцах объяснить, что и зачем делается в этих multigrid-методах?