Линейная алгебра, минимизация нормы

[stanger]

Есть задача:
Матрицы $A$ и $B$ одинаковой размерности. Нужно найти такую ортогональную матрицу $Q$, что $||QA-B||_F$ минимальна. $F$ - норма Фробениуса.

Мое решение: найдем вместо минимума $||QA-B||_F$ минимум $||QA-B||^2_F$. Минимум будем находить с помощью метода множителей Лагранжа с условием $E - QQ^T = 0$

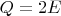
В итоге я получил $Q(2AA^T+L^T+L) = 2BA^T$. как отсюда выразить $Q$?пробовал просто транспонировать это равенство и перемножить их, получил $(2AA^T+L^T+L)^T(2AA^T+L^T+L) = (BA^T)^T(BA^T)$. Отсюда $Q = 2E$. А это какая-то ерунда! Помогите разобраться, пожалуйста.

[Brukvalub]

stanger в сообщении #1169390 писал(а):

В итоге я получил $Q(2AA^T+L^T+L) = 2BA^T$

Давайте сначала предложим форумчанам догадаться, что такое $L$! Экстрасенсы, вперед! Форум в вас верит!

[stanger]

$L$ - это собственно матрица, образованная из множителей Лагранжа.

То есть, вообще говоря, функция Лагранжа выглядит следующим образом:

$L(Q, \lambda) = ||QA-B||_F^2 - \sum_{ij}\lambda_{ij}(E-QQ^T)_{ij}$

Перепишем это в матричном виде $L = (\lambda)_{ij}$:

$L(Q, \lambda) = \operatorname{tr} ((QA-B)^T(QA-B))- \operatorname{tr} (L^T(E-QQ^T))$

Отсюда мы должны взять производную по $Q$ и приравнять ее к 0.
У меня получилось: $QAA^T + QAA^T - BA^T - BA^T + (L^T+L)Q = 0$
Что я делаю не так?

[Brukvalub]

stanger в сообщении #1169466 писал(а):

Что я делаю не так?

Вы не так излагаете свои попытки решения. Чтобы вас проверить, кому-то нужно восстановить пропущенные вами куски. Это имеет смысл делать, когда я читаю научную статью. Но зачем мне так корячиться, чтобы найти вашу ошибку? Предложите мне хотя бы одну разумную причину для этого, и я сразу же кинусь к столу с ручкой и бумагой!

[Xaositect]

stanger в сообщении #1169466 писал(а):

У меня получилось: $QAA^T + QAA^T - BA^T - BA^T + (L^T+L)Q = 0$

Уравнение правильное. Непонятно, как Вы сделали вот этот вывод:

stanger в сообщении #1169390 писал(а):

получил $(2AA^T+L^T+L)^T(2AA^T+L^T+L) = (BA^T)^T(BA^T)$. Отсюда $Q = 2E$.

Из написанного Вами соотношения надо выражать $L$ (а точнее, какое-нибудь удобное подвыражение с участием $L$), а из него уже $Q$.

[stanger]

я уже разобрался, спасибо.

данное равенство $QAA^T + QAA^T - BA^T - BA^T + (L^T+L)Q = 0$ я домножил на $Q^T$ справа. Получил $2AA^T + Q^T(L^T+L)Q = 2Q^TBA^T$. Затем транспонируем полученное равенство: $2AA^T+Q^T(L+L^T)Q = 2(BA^T)^TQ$. Вычтем из одного второе, получим, $Q^TBA^T = (BA^T)^TQ$. Ну отсюда уже и достанем $Q$