Двойной мост Томсона

[StaticZero]

При балансировке измерительного моста Томсона (см. схему) можно ввести условие баланса $I_g = 0$ априори и решить систему уравнений законов Кирхгофа, чтобы посмотреть, как должны соотноситься сопротивления элементов.

(Схема)

Написал такую систему:

$$ \begin{cases} I_1 R_1 - I_2 R_2 - r I_r = 0, \\ I_3 R_3 - I_4 R_4 - x I_x = 0, \\ I_2 R_2 + I_4 R_4 - I R = 0, \\ I_1 = I_3, \\ I_2 = I_4, \\ I_r = I + I_2, \\ I_x = I + I_4, \end{cases} $$

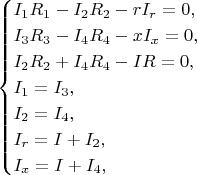
упростил до

$$ \begin{cases} I_1 R_1 - I_2 R_2 - r I_r = 0, \\ I_1 R_3 - I_2 R_4 - x I_r = 0, \\ I_2 R_c - R I_r = 0, \\ \end{cases} $$

где $R_c = R + R_2 + R_4$. Запишу в виде матрицы:

$$ \begin{pmatrix} R_1 &\ -R_2 &\ -r \\ R_3 &\ -R_4 &\ -x \\ 0 &\ R_c &\ -R \end{pmatrix} \begin{pmatrix} I_1 \\ I_2 \\ I_r \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix}. $$

Выписанное везде в методичках условие баланса

$$ x = \dfrac{r R_3}{R_1} + \dfrac{R R_2}{R + R_2 + R_4} \left( \dfrac{R_3}{R_1} - \dfrac{R_4}{R_2}\right)$$

обращает определитель матрицы системы в нуль, что легко проверить.

А как тогда быть с физическим смыслом, ведь ток в цепи тогда вообще не идёт, так как $I_1 = I_2 = I_r = 0$ и других решений нет?

[Ms-dos4]

StaticZero
Ничего себе. Наоборот, в однородных СЛАУ нетривиальное решение есть только тогда, когда определитель матрицы коэффициентов есть нуль.
P.S.В данном случае, заданное $\[x\]$ не обращает определитель в нуль. Так что либо ошибка в методичке, либо вы неверно записали систему уравнений.

[StaticZero]

Тьфу. Тривиальное решение единственно только тогда, когда ядро матрицы системы имеет размерность нуль. А размерность нуль значит, что $\det \ne 0$.

А отрицание этого утверждения у меня сделать не получилось
$\det = 0$ означает, что $\dim \ker \ne 0$, и есть нетривиальные решения. Вот так, видимо, правильно. И вопрос сам собой отпадает.