Как обозначать матрицу, составленную из векторов?

[egslava]

Здравствуйте! Буду очень рад, если подскажете с обозначениями!

Допустим, есть последовательность векторов $X = (\vec{x_1}, \vec{x_2}, \dots, \vec{x_n})$ одинаковой размерности. Т.е. $\vec{x_i} = (x_{i1}, x_{i2}, \dots, x_{im})$

Какая есть форма записи вот такой вот матрицы A, у которой i-ая строка является i-ым элементом (вектором) из последовательности X?

Т.е. можно ли записать такую матрицу: $A = \begin{pmatrix} x_{11} & x_{12} &\dots & x_{1m} \\ x_{21} & x_{22} &\dots & x_{2m} \\ \cdots & \cdots & \cdots & \cdots \\ x_{n1} & x_{n2} &\dots & x_{nm} \\ \end{pmatrix}$ вот так: $A = \begin{pmatrix} \vec{x_1} \\ \vec{x_2} \\ \vdots\\ \vec{x_n} \\ \end{pmatrix}$

?

[mihailm]

Конечно можно. Стрелочки правда часто заменяются на полужирный шрифт.

[arseniiv]

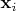
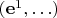
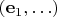
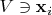
Выглядит достаточно прозрачно, но $\mathbf x_i$ должны обязательно быть строками. Если это столбцы, их надо транспонировать, а если это «просто» векторы, то лучше бы получение компонент в каком-то базисе записать явно, иначе запись, строго говоря, некорректна. 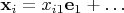Впрочем, если $(\mathbf e^1,\ldots)$ — базис, сопряжённый базису $(\mathbf e_1,\ldots)$ в $V$, $V\ni\mathbf x_i$, компоненты в котором и даны: $\mathbf x_i = x_{i1}\mathbf e_1 + \ldots$, то ваша матрица будет иметь и совершенно* корректную запись

$$\begin{bmatrix} \mathbf x_i \\ \vdots \end{bmatrix} \begin{bmatrix} \mathbf e^1 & \cdots \end{bmatrix},$$

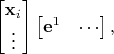
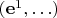
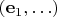
причём если $V$ у нас со скалярным произведением, то мы, конечно, можем вместо $(\mathbf e^1,\ldots)$ взять $(\mathbf e_1,\ldots)$ и умножать векторы скалярным произведением.

* К этой тоже можно придраться, но это труднее.