Князь Хорошевский Клюж утверждал, что нашел три квадратных трехчлена:

, у которых

, имеющих по два корня каждый.Не ошибся ли он?
Ошибся.
1)Для

верно,

2) Пусть

, тогда

, поэтому второе уравнение не имеет корней. Аналогично рассуждаем для

и

3) Если
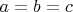
, то, очевидно, ни одно ур-е не имеет решений.
Правильно ли мое решение?