Первое, что сразу же напрашивается, можно пренебречь слагаемым

в сумме

Хочу рассказать, почему так делать нельзя. Аргумент функций Эйри буду обозначать

(вещественное число), чтобы не путать с Вашим

.
При

для

справедливы асимптотические формулы:

При больших отрицательных

обе функции совершают колебания с медленно растущей (в сторону отрицательной бесконечности) частотой и медленно убывающей амплитудой. Введём понятие фазы

— это аргумент синуса и косинуса (без константы
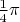
).
В Вашем выражении функции Эйри берутся от двух аргументов:

и

. Им соответствуют фазы


Выясним, как ведёт себя разность этих фаз при

и фиксированном

. Заранее сказать трудно, потому что здесь противоборствуют два фактора: рост

увеличивает разность фаз, а убывание слагаемого

— уменьшает. Вычисление показывает, что разность фаз стремится к константе

. Значит, если при некотором достаточно малом

функции

совершают десять колебаний между

и

, то и при любом как угодно малом

они будут делать между

и

те же десять колебаний, и пренебрегать слагаемым

нельзя.