Существует ли гармоническая функция

[polevoy]

Существует ли положительная гармоническая функция $u$ на открытом единичном шаре в $R^3$, такая что $u(0, 0, 0)=1$, $u(0, 0, 0.5)=10$?

[venja]

Например, взять функцию вида
$U=\frac A{\sqrt{x^2+y^2+(z-5)^2}} +B$
и подобрать 2 параметра так, чтобы выполнялись заданные условия в точках.

[polevoy]

venja писал(а):

Например, взять функцию вида
$U=\frac A{\sqrt{x^2+y^2+(z-5)^2}} +B$
и подобрать 2 параметра так, чтобы выполнялись заданные условия в точках.

Указанная Вами функция не будет положительной на единичном шаре. Действительно, находим $A=405$, $B=-80$. Поэтому в некоторой окрестности точки $(0, 0, -1)$ функция строго отрицательна.
По-видимому, нужно доказать, что такой функции не существует.

[Echo-Off]

Если под открытым единичным шаром понимается единичный шар с центром в 1 $B_1(0)$, то такой функции не существует по теореме о среднем. А именно:
Берём маленькое $\varepsilon>0$. Тогда

$$ \iiint\limits_{B_{1-\varepsilon}(0)} u(x)\,dx = \frac {4\pi}3 (1-\varepsilon)^3 $$

$$ \iiint\limits_{B_{1/2-\varepsilon}(0,\,0,\,0.5)} u(x)\,dx = 10\ \frac{4\pi}3(\frac 12}-\varepsilon)^3 $$

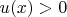
Так как $u(x)>0$, то первый интеграл должен быть больше второго. Однако раз плюнуть подобрать такое $\varepsilon>0$, чтобы это было неверно.
Может возникнуть вопрос: зачем эти $\varepsilon$, почему сразу нельзя взять интеграл по шарам $B_1(0)$ и $B_{\frac 12}(0,\,0,\,0.5)$. Ответ: потому что в теореме о среднем по шару предполагается, что $u$ непрерывна вплоть до границы шара.

[polevoy]

Echo-Off писал(а):

такой функции не существует по теореме о среднем

Спасибо большое!