Метрики и эталоны или эталоны и метрики

[SomePupil]

Прохожу курс аналитической геометрии по Постникову. Там развивается теория внешних произведений векторов. В частности, вводятся определения длины, площади, объема через эталоны обычного вектора, 2-вектора и 3-вектора. После этого идут метрики, то есть, на векторном пространстве определяется функция, удовлетворяющая аксиомам метрики (она и есть метрика).

И вот появился вопрос, как это все можно согласовать.

Конкретно: ну, вычислю я площадь параллелограмма по метрике: найду длины сторон параллелограмма, угол между ними, умножу на синус, то да сё. Потом вычислю по-другому: введу "эталон площади" $-$ произвольный 2-вектор. Найду соответствующий коэффициент пропорциональности и объявлю, что это и есть искомая площадь.

Будут ли эти площади равны? Очевидно, что при выборе эталона (как и метрики) есть произвол. Но наверняка можно специально выбрать такой эталон (2-вектор) и метрику, что площади всегда будут получаться равными. Вопрос только в том, как именно выбирать? И еще: для того, чтобы развить теорию внешних произведений векторов, необязательно работать с действительными числами, тогда как теория метрики основывается именно на $\mathbb R.$

Получается, можно рассматривать площади, объемы с точки зрения различных вещей (метрик, внешних произведений, мер(?)), и не факт, что эти точки зрения будут согласованы между собой. Так?

P. S. При выборе эталона, получается, мы неявно вводим определенную метрику. Неплохо было бы упомянуть это в учебнике (в скобках).

[svv]

SomePupil в сообщении #1161905 писал(а):

Будут ли эти площади равны?

Не обязательно.

SomePupil в сообщении #1161905 писал(а):

Получается, можно рассматривать площади, объемы с точки зрения различных вещей (метрик, внешних произведений, мер(?)), и не факт, что эти точки зрения будут согласованы между собой. Так?

Да, так.

SomePupil в сообщении #1161905 писал(а):

Вопрос только в том, как именно выбирать?

Эталон длины согласован с эталоном ($n$-мерного) объёма, если объём $n$-мерного куба со стороной $1$ равен единице.

SomePupil в сообщении #1161905 писал(а):

При выборе эталона, получается, мы неявно вводим определенную метрику.

Нет. Для измерения $n$-мерных объёмов в $n$-мерном пространстве не нужна метрика, нужен только эталон объёма.

Для измерения $k$-мерных объёмов в $n$-мерном пространстве ($k<n$) метрика нужна. Чуть подробнее: Вы можете, скажем, на некоторой $k$-мерной плоскости ввести эталон $k$-объёма, но без метрики Вы не сможете «перенести» его на другие $k$-плоскости, не параллельные данной.

[arseniiv]

SomePupil в сообщении #1161905 писал(а):

ну, вычислю я площадь параллелограмма по метрике: найду длины сторон параллелограмма, угол между ними, умножу на синус, то да сё

Если точнее, это не совсем «по метрике». Это применение доказанной связи меры (согласованной со структурой евклидова пространства) параллелограмма с расстояниями между его вершинами.

[Munin]

SomePupil в сообщении #1161905 писал(а):

Конкретно: ну, вычислю я площадь параллелограмма по метрике

По метрике нельзя вычислить площадь. Можно только длину. А площадь - ну мало ли какая она там ещё будет.

Тут математика спотыкается на том, что если у нас не дано определения какой-то вещи, то этой вещи ещё и нет. Наивно мы восклицаем: "ну очевидно же, что площадь прямоугольника $S=ab$!" А математик отвечает: "нет, вот что такое длина, у меня есть определение и метод вычисления, а что такое площадь - я пока не знаю".

Поэтому, кроме метрики, вводятся дополнительные функции, сопоставляющие каким-то площадкам их площади, каким-то телам их объёмы, и так далее. Эти функции могут опираться на метрику, а могут и не опираться. И вводиться они могут очень по-разному.

Простой пример, не совпадающий с "самоочевидным". Допустим, у вас на плоскости $(x,y)$ задана положительная непрерывная функция $\rho(x,y)$ - плотность картона, и то, что мы называем "площадью" фигуры, на самом деле будет весом этой фигуры, когда мы её из этого картона вырежем. Тогда площадь прямоугольника будет вовсе не $S=ab,$ а $S=\int_a\int_b \rho\,dx\,dy.$ Но с метрикой от этого ничего не случится! Стороны прямоугольника по-прежнему будут по длине $a$ и $b.$

SomePupil в сообщении #1161905 писал(а):

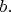
И еще: для того, чтобы развить теорию внешних произведений векторов, необязательно работать с действительными числами, тогда как теория метрики основывается именно на $\mathbb R.$

Вот это вопрос непростой и интересный. И как мне кажется, он может зависеть от выбранных определений. Мы можем потребовать, чтобы площади всегда относились к $\mathbb{R}.$ А можем - оторваться от этого требования. Это будет непросто, но как мне кажется, достижимо. Но не в каждом учебнике такое можно будет найти.

[SomePupil]

Всем спасибо!

P. S. Чем хорош этот форум, так это тем, что на конкретный вопрос можно получить конкретный ответ.